Linear-algebra-feeling

之所以起了这么一个奇怪的标题，完全是因为我是一个数学的白痴，不敢写任何数学相关的硬知识。不幸的是，在学习一些算法时，又不得不接触一些数学。尤其在机器学习领域，线性代数是一个绕不过去的话题。不像高等数学和概率，凭着一些常识和临时 Google 能蒙混过关（虽然也很艰难），线性代数甚至是很多算法的表现形式。如果不能系统的认识它，大部分算法往往不知所云。一个简单的例子，基本上机器学习领域所有的输入数据，中间数据都是矩阵来表示的，无论是图像，文本，各种算法无非是施加在上面的各种运算。

这里，我不会罗列方程与公式，甚至除了基本概念外，也不用会用精确的数学语言描述这些概念。我只是想在这里提供一种『直觉』的东西，让我们能明白，算法中代数运算的现实意义。

起步

粗略的罗列一下我们会遇到的基本概念

• 线性空间
  • 线性相关性
  • 基的概念
• 行列式 --$|A|$
  • 行列式的值（计算行列式）
  • 行列式的意义
• 向量
  • 向量的本质
  • 抽象向量空间
• 矩阵—$A$
  • 可逆（可逆的条件&&求逆矩阵）
  • 矩阵的秩（行秩&&列秩）
  • 特征值&&特征向量
  • 相似性
• 一些特别的矩阵（往往具有良好的性质）
  • 方阵（n*n 的矩阵）
  • 单位矩阵
  • 实对称矩阵
  • 对角矩阵
  • 正交矩阵
• 矩阵相关计算
  • 点积
  • 叉积
• 实践中遇到矩阵
  • 协方差矩阵

上面这些基本的概念中，尤其重要的，也是实践中最有意义就是那些特殊的矩阵，他们具有良好的性质。我们的目标往往是把一些普通的矩阵，想尽一切办法构造、转换为这些特殊的矩阵：

• 可逆的
• 正交的
• 对称的
• 再特殊点，能转换成对角矩阵

因此，除了了解基本的概念外，我们学习的目标是要掌握这些矩阵的性质和意义。

资料推荐

推荐一些不错的学习资料（入门级别），他们很少（甚至没有）的数学公式，旨在通过直观的方式理解线性带上，可以重点看前两个资料：

• 3Blue1Brown课程：线性代数的本质：十几课，每堂课十几分钟，强烈推荐先学习。
• 马同学的课程，图文并茂，0 基础可掌握，思想与上面的课程类似。
  • 行列式的本质是什么？
  • 如何理解矩阵的秩？
  • 如何理解，矩阵的秩与线性方程组的关系？
  • 相似矩阵是什么？
  • 如何理解特征值和特征向量?
• 理解矩阵：从另一个纬度理解矩阵
  • 理解矩阵(一)
  • 理解矩阵(二)
  • 理解矩阵(三)
• 其他
  • 特征值与特征向量的几何含义
  • 协方差矩阵
    • 浅谈协方差矩阵
    • 再谈协方差矩阵之主成分分析

一次线性代数之旅

现在我大致讲述一下线性代数的逻辑，需要的背景知识是曾经接触过线性代数的课程内容，现在只有一点点模糊的印象，大致知道向量，向量相加，矩阵如何表示，矩阵乘法的计算方法这几个常识（不需要理解）。

我们知道线性代数是一个非常 General 的知识，他可以应用在方方面面，从几何的角度看：从我们有认知的二维、三维空间，到我们无法感受的高纬空间。这里我只想从最最简单的空间上体会它：二维空间上的向量。最后，我们会一起探讨线性代数在向量之外的应用。

假设空间

我们首先假定一个我们讨论的空间：二维平面，即二维坐标系 x 轴，y 轴。在此基础上我们首先讨论向量这个基本概念。在不同的场景上，向量意味不同 $\left(\begin{array}{c}-2\\ 3\end{array}\right)$：

• 物理角度：它是一个有向箭头，由于（长度，角度）唯一确定，与起点，终点无关。二维向量就是平米的一个有向箭头。

• 计算机角度：在机器学习中经常使用有序的数字列表来表示一个样本的特征（数字顺序不可颠倒）。二维向量就是一个两个特征的样本。

• 在数学中：

  • 向量是一个抽象的概念（他满足某些约束就是向量）
  • 但是，这里我们从几何视角看待它：是用来表示空间中以原点为起点，以 $\left[\begin{array}{c}-2\\ 3\end{array}\right]$ 该点为终点的一个箭头（与物理视角不同，他是有固定起点的），他表示，从原点出发，先沿着 x 轴前进 -2 个单位长度，再接着像 y 轴方向前进 3 个单位长度。
  

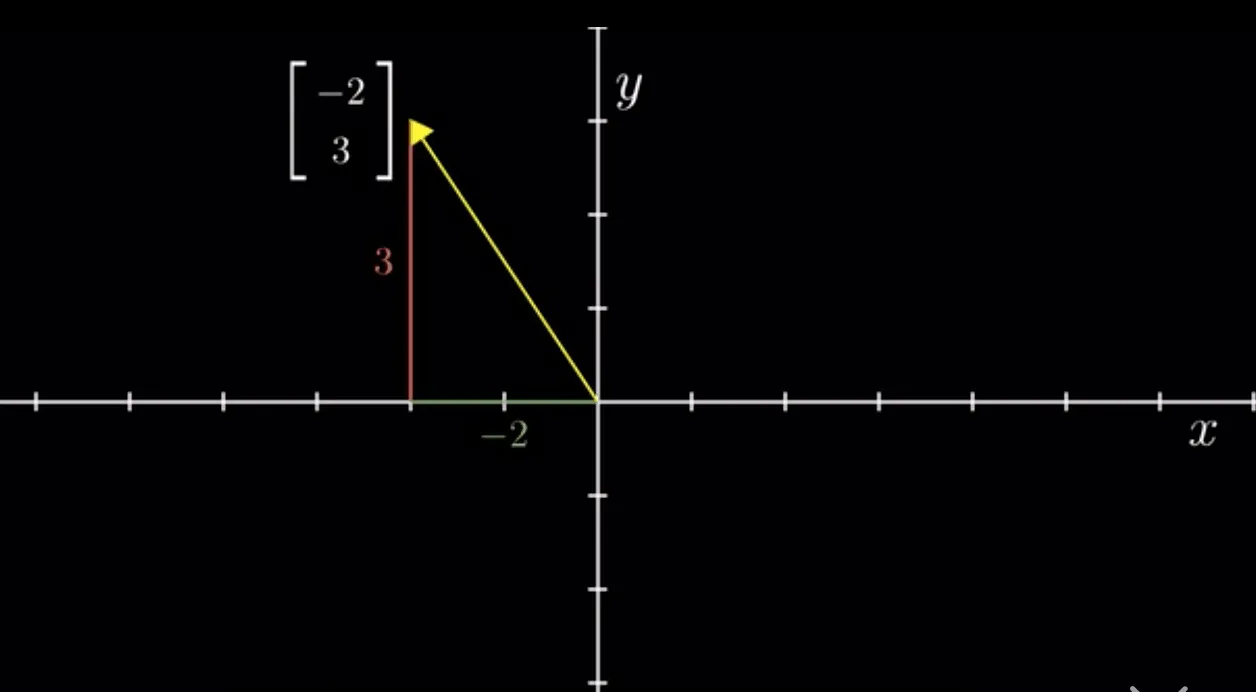
虽然我们展示了 3 种视角，但是从本质上看（抽象的角度）他们是一致的。无论什么视角，他们都满足两个基本的运算（这个我们会在最后谈论这个主题，把向量推广开去）：

• 加法运算

  

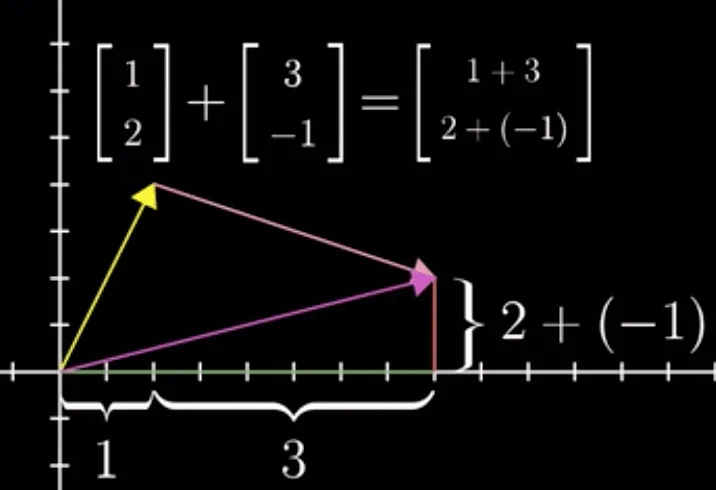
• 数乘运算

  

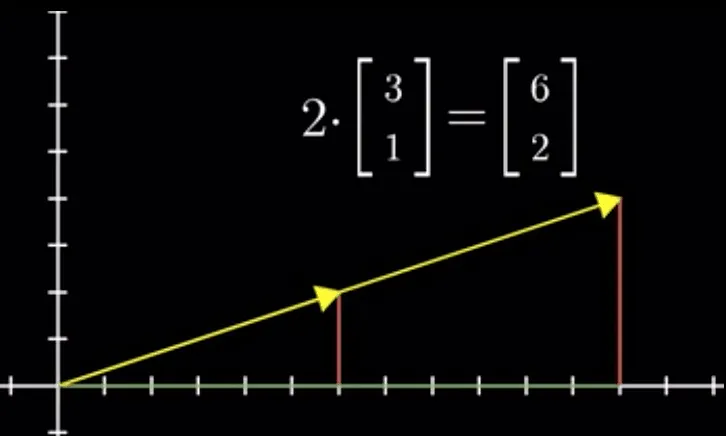
因此，下面的论述中，我们都以『几何视角』下的向量来讨论。

基底与张成的空间

在我们讨论向量时，其实我们都默认选择了一组基 i,j，他们沿着 x 轴和 y 轴方向，他们正好大小是 1。

我们选择这一组基可以表示整个二维空间，我们说这组基张成了二维的空间

不只一组基，我们可以选择其他线性无关的向量的作为基底，此时二维空间尽在掌握。

当我们『运气不好』时，选择的基底（共线，线性相关）不能张成整个二维空间，而是一条直线（一纬空间）

定义 -- 向量空间的一组基：张成改空间的一组线性无关的向量集

矩阵与线性变换

这是理解矩阵的关键。

线性变换

区分线性变换与非线性变换：线性变换要求变换后的网格：

• 原点固定
• 变换后网格依旧是直线（没有变弯）。

总之，要求变换后网格间等距&&平行。

因此可以常见的线性变换有：

• 旋转 -rotate
• 伸缩 -scale
• 剪切 -shear

线性变换的表示

一个重要的洞见是：在线性变换前可以由基底 $i$，$j$ 表示的向量 $v$（$v=ai+bj$），在变换后依然可以由他们表示（$v^{{}^{\prime }}=a\hat{i}+b\hat{j}$，其中，a,b 值不变）。因此，只要知道 $i$，$j$ 变换后的位置就能推断出任意向量的位置！！！

再推导出，一个线性变换可以由 $[\hat{i},\hat{j}]$ 唯一表示，在二维空间中该线性变换就是 4 个数字唯一确定。

由于这个推理非常重要，我们举例说明：

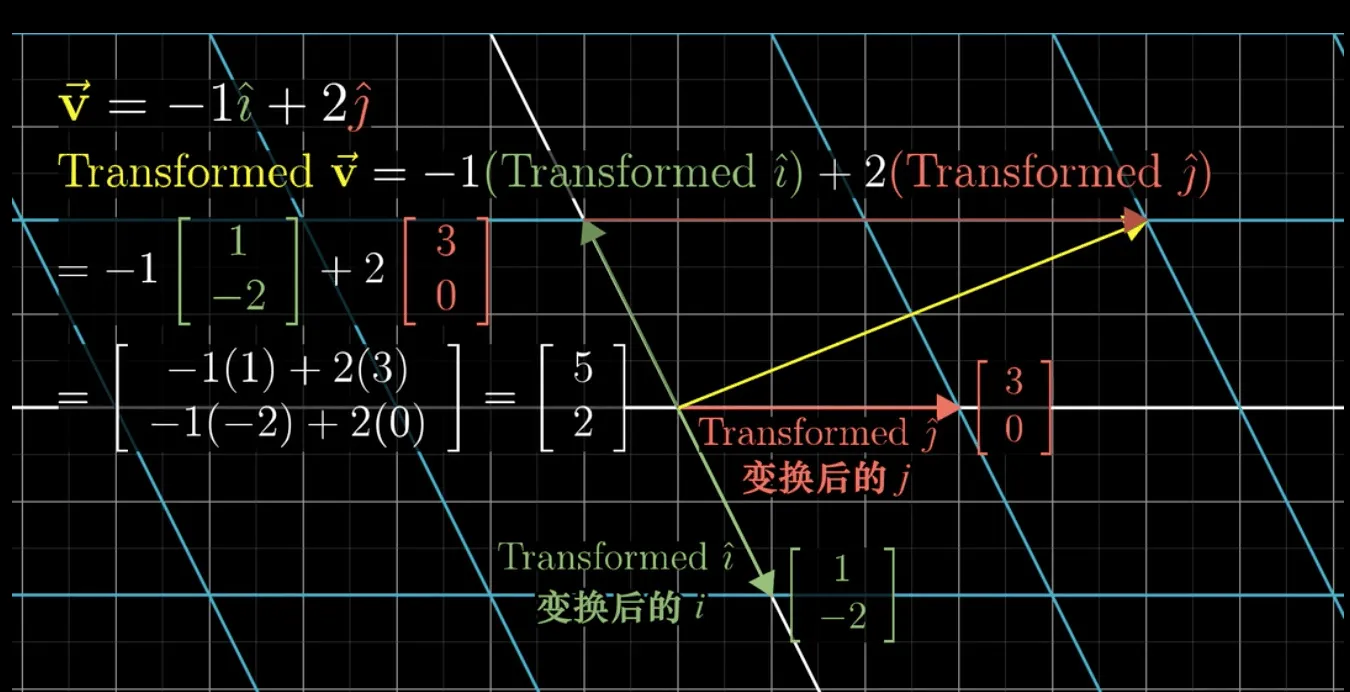
如上图所示，

初始状态下，$i$，$j$ 均在 x，y 轴上，分别为 $\left[\begin{array}{c}1\\ 0\end{array}\right]$ 、$\left[\begin{array}{c}0\\ 1\end{array}\right]$。此时，$v$ 向量在空间中坐标为 $\left[\begin{array}{c}-1\\ 2\end{array}\right]$。

经过某个线性变换后 $\hat{i}$,$\hat{j}$ 的位置分别位于 $\left[\begin{array}{c}1\\ -2\end{array}\right]$（绿色箭头） 、$\left[\begin{array}{c}3\\ 0\end{array}\right]$（红色箭头）。此时 $v^{{}^{\prime }}$ 在空间中位于新的基底组合，$-1\left[\begin{array}{c}1\\ -2\end{array}\right]+2\left[\begin{array}{c}3\\ 0\end{array}\right]$ 即 $\left[\begin{array}{c}5\\ 2\end{array}\right]$（黄色箭头）。

因此，我们可以把 $\hat{i}$ 和 $\hat{j}$ 放在一起形成一个 2*2 的矩阵，表示我们的线性变换（图上的值不对！！！）：

所以，不难得出，每当我们看到一个矩阵时，可以从得到两个信息：

• 这个矩阵代表了一个线性变换。任何一个向量与该矩阵相乘就是进行这个变换。
• 变换后的基向量发生了改变，变换到了的位置就是矩阵的列向量

一个简单的应用：我们可以使用上面的结论轻易地求得，一个把图像逆时针旋转 90 度的变换矩阵是 $\left[\begin{array}{cc}0& -1\\ 1& 0\end{array}\right]$。解释如下：我们只需要跟踪旋转后的 $i$、$j$ 坐标即可，画图后显然得到新的 $\hat{i}$ 在（0,1），新的 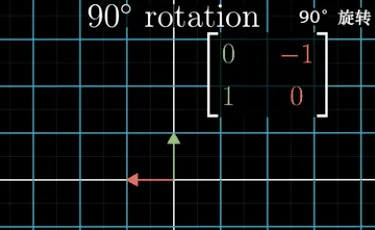$\hat{j}$ 在（-1，0）上：

从基变换的角度看矩阵（参考下面）

同样对于上面这个矩阵乘法，我们还可以从一个独特的角度看

它表示：在 ,$\hat{i}=\left[\begin{array}{c}1\\ -2\end{array}\right]$ 、$\hat{j}=\left[\begin{array}{c}3\\ 0\end{array}\right]$ 这组基底下面的坐标 $\left[\begin{array}{c}-1\\ 2\end{array}\right]$，在基底分别为 $\left[\begin{array}{c}1\\ 0\end{array}\right]$ 、$\left[\begin{array}{c}0\\ 1\end{array}\right]$ 下（我们认为的坐标系）时的坐标为 $\left[\begin{array}{c}5\\ 2\end{array}\right]$。确切的说他的形式如下：

代表了一个向量在两种基底下的表示方法。

矩阵乘法

此时，我们就很好理解多个矩阵相乘了（矩阵乘法），他表示了施加了多次的线性变换。

逆矩阵

同样，A 的逆矩阵表示了 A 的线性变换的相反的变换。但是很多情况下变换是不可逆的，原因也很简单：A 的变换可能是降维的（秩的概念，列空间），导致不可以反向变换。

矩阵的秩与线性方程组的解

让我们从线性变换的角度理解方程组的解。

当我们可以把线性方程组表示成矩阵相乘的形式：$Ax=b$（矩阵 A 中的 0 表示线性方程组中没有多余的项）

不难理解对于矩阵 $A$ 的秩不同情况，方程组的解 $x$ 的个数不同。

矩阵的秩：线性无关的列（行）的个数。矩阵行秩等于列秩。

对于 n*n 的矩阵 $A$：

• 满秩 $r(A)=n$：有唯一解 $x=A^{-1}b$，从矩阵变换角度看，A 的变换有唯一的逆变换 $A^{-1}$。
• $r(A)<n$：从矩阵变换角度看，由于 $|A|=0$ (3 维变 2 维的物理意义的体积为 0)，变换发生了压缩，没有唯一的逆变换。同时这个变换 $A$ 把任意向量 $x$ 压缩到了一个新的低维空间。
  • 有无数解，$Ax$ 相当于把高纬的 $x$ 都压缩到了一个新的空间中（$A$ 的隐含基底），$b$ 如果在这个空间里就有无数解。
    • 当向量 $b$ 在新的低维空间中时，有无数解。（想象一下，为什么是高维的无数个向量都是解，一个低纬对应无数的高纬，想象一下被拍扁了）
    • 特别地，当 $b=0$，向量 b 一定在低纬空间中（不管什么空间必须经过原点）。解空间大小为 $n-r(A)$（也称为零空间或者核），有 $n-r(A)$ 个线性无关的向量被压缩多原点。（如二维空间，有一个沿着某个方向的直线被压缩到原点，三维空间，有一个直线或者平面被压缩到）
  • 没有解，矩阵 $A$ 变换压缩到的新的低纬空间中不含有向量 $b$。

矩阵的秩：也代表了变换后空间的纬度，从矩阵代表坐标轴的角度看，他的每一列都是新空间的坐标，很容易理解，矩阵的秩就是列空间的维数。

矩阵的特性：行列式

行列式的值表示了矩阵变换的面积缩放大小，如 det(A)=0，表示面积为 0，被压扁，说明该变换导致了纬度被压缩（丢失了信息）。

特殊的线性变换：点积

• 几何意义：
  • 投影长度 $|\mathrm{被}\mathrm{投}\mathrm{影}\mathrm{向}\mathrm{量}|$
  • 满足交换率，与被投影向量无关。
• 计算方法：对应位置的坐标相乘（很像一个特殊的线性变换 -- 多维到一维的线性变换）
• 使用『对偶性』解释计算方法（线性变换）与几何意义
  • 从线性变换角度理解（使用向量代表了一个特殊的线性变换）
  • 为什么很像线性变换？
    • 含义：多维到一维的线性变换
• 理解作用：完成了从 n 维向量到数（1 纬）的映射（线性变换）

特殊的线性变换：叉积

• 两个二维向量的叉积是行列式的值（忽略，我们一把都是算 3 纬向量）
• 两个三维向量的叉积
  • 几何意义：是与三维空间平面正交的向量，向量大小是行列式的值。
  • 计算方法：参考教程
  • 我们可以使用『对偶性』解释计算方法和几何意义之间的关系

从不同的角度看线性变换：基变换

理解基变换

当我们讨论向量时，$\left[\begin{array}{c}-1\\ 2\end{array}\right]$，都隐含了一个默认的假设 -- 基向量：

• 沿 x 轴正方向的 $i$，且他的长度为 1
• 沿 y 周正方向的 $j$，且他的长度为 1

但是，其实 $\left[\begin{array}{c}-1\\ 2\end{array}\right]$ 可以是任何一组基底下的向量，例如，他可能是 $\left[\begin{array}{c}2\\ 1\end{array}\right]$、$\left[\begin{array}{c}-1\\ 1\end{array}\right]$ 这组基下的一个向量 。此时他在我们默认坐标系 $\left[\begin{array}{c}1\\ 0\end{array}\right]$ 、$\left[\begin{array}{c}0\\ 1\end{array}\right]$ 下的表示的坐标计算过程如下:

我们可以从另外一个角度理解基底变换的过程：我们先误认为$\left[\begin{array}{c}-1\\ 2\end{array}\right]$ 是坐标系 $i=\left[\begin{array}{c}1\\ 0\end{array}\right]$ 、$j=\left[\begin{array}{c}0\\ 1\end{array}\right]$ 下的坐标，此时，我们通过线性变换把 $\left[\begin{array}{cc}2& -1\\ 1& 1\end{array}\right]$ 把坐标轴 $i$、$j$（基坐标）分别变换到了新的位置 $\hat{i}=\left[\begin{array}{c}2\\ 1\end{array}\right]$、$\hat{j}=\left[\begin{array}{c}-1\\ 1\end{array}\right]$（他们也是用默认坐标系表示的），即 $\left[\begin{array}{cc}2& -1\\ 1& 1\end{array}\right]$。此时，我们把误解转换为了真正的向量。图示如下：

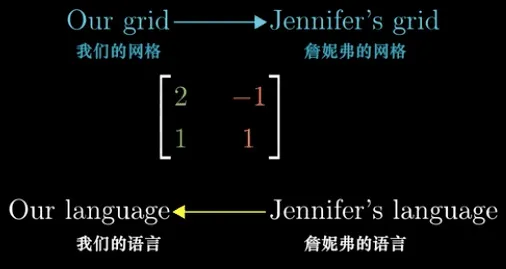
总结一下：理解计算过程

• 几何上看：这个矩阵表示把我们的默认坐标系转换为新的基坐标系
• 数值上看：把其他基底表示（Jennifer 的语言）的坐标 $\left[\begin{array}{c}-1\\ 2\end{array}\right]$ 转换成默认基底标识（我们的语言）的坐标 $\left[\begin{array}{c}-4\\ 1\end{array}\right]$

相反地，如果我们已知某个向量默认坐标系下的表示，需要得到他在其他基底下的表示则是一个逆过程。

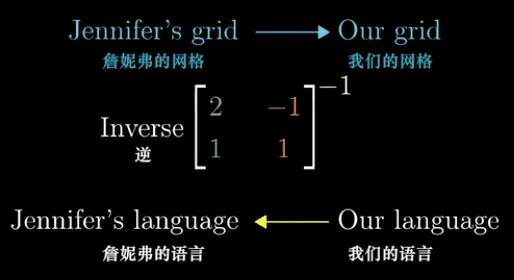
因此，我们获得了从另外一个角度理解 矩阵 * 向量（$Ax=y$）的方法（之前的角度是线性变换）：

把矩阵 $A$ 看做一个声明，它是向量 $x$ 的的基坐标，$Ax$ 的结果 $y$ 是在默认基底下 y 的坐标系，可以这样看等式：$Ax=Iy(I\mathrm{为}\mathrm{单}\mathrm{位}\mathrm{矩}\mathrm{阵})$

理解相似

思考一个问题：如何把一个非标准基底表示的向量（上面的 $\left[\begin{array}{c}-1\\ 2\end{array}\right]$，或任性向量 $v$）旋转 90 度，他的矩阵是什么？

我们已经知道对于标准基之下很容易就知道这个矩阵 $\left[\begin{array}{cc}0& -1\\ 1& 0\end{array}\right]$（参考上面一节）。可是我们并不能直接把他应用到非标准的基底上。理论上我们可以用类似的思想：跟踪在非标准坐标系下的 $i$、$j$ 坐标的的取向来确定。但是这很不直观。更为常用的作法是把它转换到标准坐标系后执行旋转，最后再转换回非标注坐标系，参考下图：

此时，我们对非标准坐标系下的任意向量 $v$ 执行变换 $\left[\begin{array}{cc}1/3& -2/3\\ 5/3& -1/3\end{array}\right]$ 等价于在标准坐标系下执行对象向量 $v^{{}^{\prime }}$ 执行 $\left[\begin{array}{cc}0& -1\\ 1& 0\end{array}\right]$ 变换（数学上我们叫这两个矩阵相似）。（PS：反过来也等价，我们可以把一个在标准坐标系下负责的变换转换成非标准坐标系看起来简单的变换，如对角矩阵，参考下面的『特征基』）

通用化这个结论： (帮助我们理解下面的特征值和特征向量！就是当 A 为特征向量的特殊情况)：

每当我们看到 $A^{-1}MA$ 这个矩阵变换时，他暗示了，我们在非标志坐标系 $A$ 下执行的 $M^{{}^{\prime }}$（即 $A^{-1}MA$ 的值）这个变换，等价于在标准坐标系下执行 $M$ 这个变换。

矩阵的特性：特征值与特征向量

理解特征值与特征向量

我们从二维空间（平面上）内的变换 $A=\left[\begin{array}{cc}3& 1\\ 0& 2\end{array}\right]$ 来感受一下特征值和特征向量。
如果我们从平面内选 n 个向量 $v$，逐个应用上面的变换 $A$。你会发现有两种类型的向量 $v$

1. 向量 $v_1$ 变换后的 $v_1^{{}^{\prime }}$ 偏离了原来的方向（如下：粉红色是 $v_1$，黄色是 $v_1^{{}^{\prime }}$）

   

2. 向量 $v_2$ 变换后的 $v_2^{{}^{\prime }}$ 他们两者保持了统一方向：即 $v_2^{{}^{\prime }}$ 依旧留在 $v_2$ 张成的空间里（$v_2$ 张成的向量空间是一条直线）

   

显然，我们能感受到：情况 1 是普遍的，而情况 2 是特殊的。我们定义：情况 2 对于的向量 $v_2$ 就是特征向量，而 $v_2$ 与变换后的 $v_2^{{}^{\prime }}$ 的长度变化（$len(v_2^{{}^{\prime }})/len(v_2)$）就是特征值。可以看出特征值和特征向量是由矩阵本身决定的。

特征向量的个数

首先，我们直观的理解特征量的个数，然后通过方程组解的角度考察。

直观感受

对于上面的例子 $\left[\begin{array}{cc}3& 1\\ 0& 2\end{array}\right]$，可能有多条特征向量：除了上面情况 2 那个空间的所有向量（他的效果 - 特征值是把向量拉升 2 倍），我们能看出（从列向量的角度），沿着 x 轴的所有向量也是特征向量，他的效果 - 特征值是把向量拉升 3 倍。所有特征向量如下所示，他也告诉我们：除此之外的其他向量在变换的过程中或多或少都有旋转。

这里隐含了一个结论：**如果矩阵有 n 个不同的特征值，那么他们必定至少有 n 线性无关的特征向量。之所以是至少，是因为有可能特征值相同，但是特征向量不共线。

一个应用：三维空间中旋转一个图像的旋转矩阵 A（思考什么是旋转矩阵），可以通过特征向量找到他的旋转轴（特征值为 1）。

另外一个例子是：二维平面的旋转矩阵 $\left[\begin{array}{cc}0& -1\\ 1& 0\end{array}\right]$：更具特征向量的定义，你会发现二维空间中的旋转矩阵没有特征向量。因为在二维中，对于旋转这个动作来说，没有一个向量会保持方向不变。下面我们再从解方程组的角度思考

方程组的角度

根据特征向量的定义，我们可以得到 $A\overrightarrow{v}=\lambda \overrightarrow{v}$，解该方程组就能求解

对于上面的第一个例子 --$\left[\begin{array}{cc}3& 1\\ 0& 2\end{array}\right]$：2 个不同的解（特征值），对应不同的特征向量。

对应上面第二个例子 -- 旋转变换 $\left[\begin{array}{cc}0& -1\\ 1& 0\end{array}\right]$：没有实数解，没有特征向量。

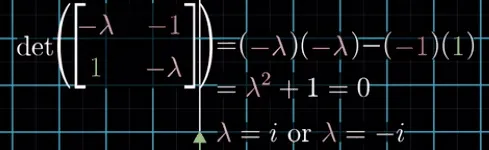
举一个只有一个特征值，且只有一个特征向量的例子 -- 剪切变换 $\left[\begin{array}{cc}1& 1\\ 0& 1\end{array}\right]$：

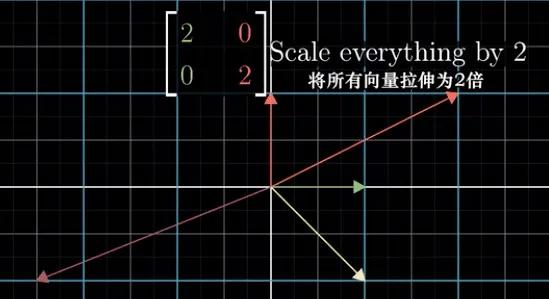
举一个只有一个特征值，但是有无数个特征向量的例子—同等拉伸变换 $\left[\begin{array}{cc}2& 0\\ 0& 2\end{array}\right]$：

可以看一下其他三维矩阵的几个 典型例题，我们知道，在特征值不同时，矩阵的特征向量的个数与特征值个数相同，在特征值相同时（二重特征值），特征向量的个数要把特征值带入方程组看解空间的大小。

特征基：使用特征向量作为基向量

对于矩阵 A（看成标准坐标系下的某种变换），如果存在 n 个线性无关的特征向量，使用特征向量作为一组基—>结合『基变换』—>转换为以 n 个特征向量为基底的某个对角变换，其中对角线的值即为特征值。如下图所示：我们把标准坐标系下的 $\left[\begin{array}{cc}3& 1\\ 0& 2\end{array}\right]$ 变换为 $\left[\begin{array}{c}1\\ 0\end{array}\right]\left[\begin{array}{c}-1\\ 1\end{array}\right]$ 为基坐标下的变换 $\left[\begin{array}{cc}3& 0\\ 0& 2\end{array}\right]$。这是一个对角变换具有良好的性质

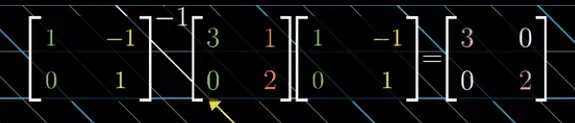
通过特征值的几何意义，我们知道，他就是某个坐标系（特征基）下的 scale 变换。由此，特征向量的意义：摆脱原始坐标轴（转而用任意特征基坐标轴）考察矩阵表示的变换。

上面变换的一个典型应用是：如果我们需要在标准坐标系下做一万次 $\left[\begin{array}{cc}3& 1\\ 0& 2\end{array}\right]$ 变换，计算是非常麻烦的，但是他和一万次 $\left[\begin{array}{cc}3& 0\\ 0& 2\end{array}\right]$ 变换等价！！（当然，做完后要变换回标准坐标系下面）

从应用的角度说，当我们对一个矩阵求特征值和特征向量的时候，可以这么理解：我们的目的是把这个矩阵（变换）寻找一个新的坐标系（就是特征向量的坐标系），在这个坐标系下还原了他的本来面目：就是计算一个 scale 缩放（特征值）

推广到 N 纬空间，对于 N 纬空间的变换 $A$，如果我们把一个 N 纬空间看做是由无数个这个空间的向量 $v$ 组成，我们把这些向量一个个都应用变换 $A$ 来测试。特征值与特征向量描述了一个高维空间变换 $A$，对某些向量张成的低纬空间（确切的说是一维空间，即由 $v$ 张成的空间，即共线的直线）的变换具有的特征。可以用『特征基』的表达式定量描述出来。用机器学习中 PCA 的术语来说，这种特征向量与特征值就是是矩阵 A 的组成成分。

抽象的向量空间

最后，让我们泛化了线性代数的概念。数学是抽象的艺术，我们希望定义一种概念，它可以包含所有我们讨论的不同领域中的概念和运算。

可以定义一个向量空间中的线性运算都可以适用线性代数的计算方法与结论。

因此我们一步一步泛化之前的概念：

• 向量：『以原点为起点』的箭头
• 线性变换：矩阵乘法运算
• 向量空间：一组基底张成的空间

泛化向量

之前我们讨论过（参考假设空间一节），无论他们是

• 物理中的箭头
• 计算机中的数字列表
• 本文讨论的『以原点为起点』的箭头

都满足，加法运算与数乘运算，我们泛化到甚至是

• 函数：
  • $(f+g)(x)=f(x)+g(x)$
  • $(2f)(x)=2f(x)$

泛化线性变换

同时，类似矩阵运算的性质，他是把一个向量变成另一个向量，同时变换前后满足下列性质：

• 可加性：$L(\overrightarrow{v}+\overrightarrow{w})=L(\overrightarrow{v})+L(\overrightarrow{w})$
• 成比例：$L(c\overrightarrow{v})=cL(\overrightarrow{v})$

我们定义，只要一个『运算 L』满足上面的性质，我们称之为线性的。

对比，函数中，可以发现函数中的变换是把一个函数变成另一个函数：『求导』运算满足上述两个特点。

泛化向量空间

在之前讨论的内容中，我们把一组基底张成的空间，当做向量空间。同样这里，我们把一组函数（这里是无穷多个）张成的空间表示为使用多项式空间，他也是一个向量空间。如 $b_0(x)=1$、$b_1(x)=x$、$b_2(x)=x^2$、$b_3(x)=x^3$.....组成了多项式空间。

多项式空间，以及之上的线性变换（导数）运算如下：

泛化向量空间上的概念与性质

基于上面的定义，函数、求导、多项式空间。我们可以泛化出对于的性质

定义抽象向量与空间

如果你处理的对象（『向量』）具有『相加』和『数乘』的性质，并基于他定义『线性变换』和『向量空间』，我们想由此推导出我们上面提到『零空间』『特征向量』『点积』等等概念。需要定义的『向量』满足下列 8 条公理：

结论：向量可以是任何东西。包括：一个箭头、一组数，一个函数，任何满足上面性质的东西。

忽略的内容

• 逆矩阵的计算方法：这里我们只介绍了您的几何意义，可以计算出常见的 2*2 的简单矩阵的逆（如旋转，scale 等）。对于复杂的变换，或者更高纬度的矩阵的逆的计算方法建议直接使用计算机。
• 求解线性方程组的解：
  • 可逆的参数矩阵 -->唯一解 -->矩阵运算
  • 消元法

总结

矩阵的两种视角

• $Av$ 可以理解为在某一个坐标系下（默认 $E$）对向量 v 的施加的运动（变换）$A$
• $Av$ 也可以理解为坐标系 $A$ 下的向量 $v$（列向量是一组基）

两者可以结合理解：运动相当于把一组标准基底 E 转换到新的基底 A-->列向量就是转换后的一组基

扩展：矩阵可以理解为任一个坐标系（一组基）下的某个运动（相似的概念）

理解矩阵

• 理解对角矩阵
  • 看做运动：对 x，y 缩放（scale 的矩阵）没有发生形变
  • 看做坐标轴：一个被拉伸的坐标系
• 理解正交矩阵
  • 看做坐标系：空间中任意一组相互垂直（正交）基，
  • 看做运动：旋转（随着坐标系旋转，需要 $|A|=1$, 等于-1 则有反转）
• 理解实对称矩阵：
  • 看做某个坐标系下的运动：可以对角化 $P^{-1}AP=V$ --> 可以看做在坐标系 P 下的 V 运动，其中，P 是正交基，V 是对角矩阵，是形变运动。即对称矩阵代表着在某个正交坐标系下的形变运动！！
    • 为什么是正交基。因为实对称矩阵必然有一组线性无关的基底，因此可以正交化。由于特征向量的性质，对角化并不影响特征值所以上式依然成立。
    • V 是对角矩阵，表示了在坐标系 P 下的运动。

至此，线性代数的入门文章已经完成，希望这些基本概念的 Feeling 能有助于你理解它在各个领域的应用。在机器学习中，数据降维常用的 PCA 与 LDA 都有涉及这些运算。理解他们是了解算法原理的第一步。