graph-algorithm-community-detection
在我们常见的数据结构中,图是一种有点冷门,时常被忽视的数据表达方式。大部分场景下,我们的数据关系足够简单,例如,一对一,一对多,这种情况下,表结构(关系数据库)或者文档结构(文档数据库)足以刻画数据之前的关系,对于稍复杂的关联/嵌套数据,通过 join 和文档嵌套的方式也可以轻松构建,此时在抽象层面,我们可以把数据的结构看作是一个树结构(数仓中也称为星型模型和雪花模型 )。那什么时候会用到图呢?答案是在数据中存在大量多对多的模式(Pattern)时,我们可以应用图数据结构(图数据库)来刻画和解决现实世界的问题。典型的图分析场景有:
- 网络关系的表达与相关优化:社交网络,通讯网络,交通网络
- 推荐算法:网页排序,相似用户推荐
- 关联分析与数据洞察:关键节点分析
- 无监督/半监督学习:社区聚类与挖掘,样本标注
- 数据可视化:可视化数据的关系
下面我们从图的基础概念出发,分别介绍在单机与分布式环境下的图的存储方法,图分析的常见算法。此外,还会重点分析一些图算法的分布式实现以及社区挖掘的应用。
这里主要介绍的内容来自于
- 场景图算法以及单机实现来自于流行的图数据库 neo4j
- 分布式的实现参考 Spark GraphX
- 图的可视化工具使用 Gephi
图基本概念与算法
图在数据结构中多少都有一些接触,下面我们自行回忆一下图的基本概念:
- 图的定义:
,其中 是顶点 (Vertex) 的非空有限集合, 是连接V中两个不同顶点(顶点对)的边的有限集合 - 边与权重、邻接点
- 有向图 vs 无向图
- 稀疏图 vs 稠密图
- 完全图
- 入度 vs 出度
- 连通图 vs 非连通图、图的连通分量
- 生成树、生成森林
图的表示方法
图的基本表示方法有
-
邻接矩阵:使用一个
的矩阵表示图(N 是顶点数),对应的值表示边,适合表示稠密图 -
邻接表 :数组与链表相结合的存储方法,数组中为图中的顶点,所关联的链表是与该顶点连接的边,适合表示稀疏图
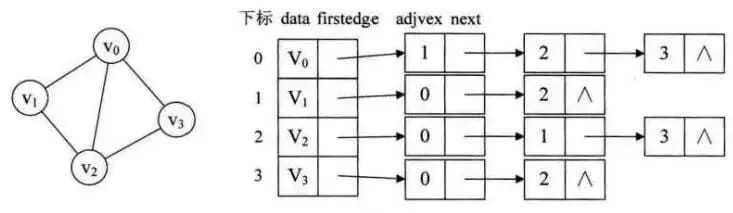
-
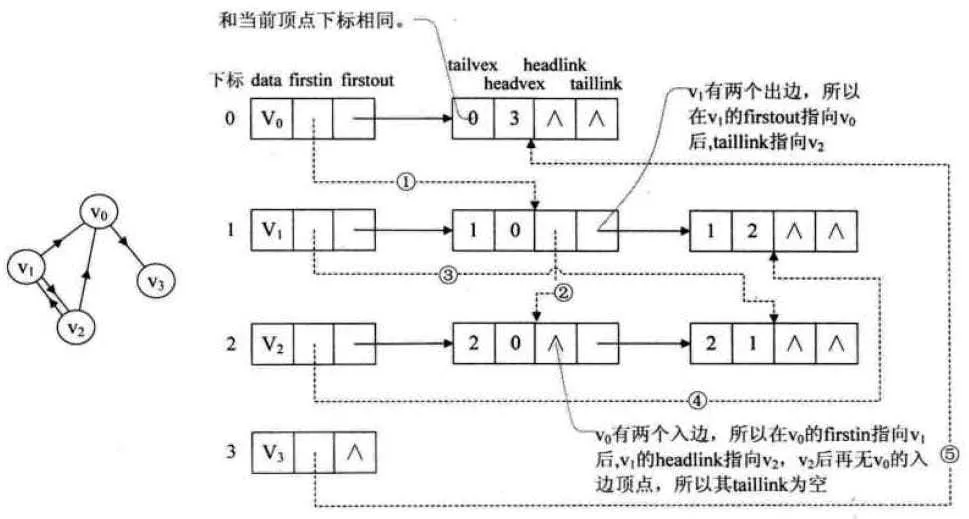
十字链表法:是邻接表的改进方法,对于有向图,便于快速计算入度与出度。
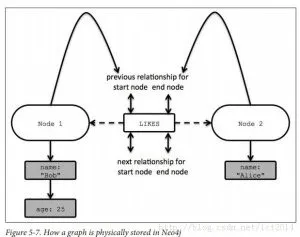
在 neo4j 数据库中使用了类似邻接表的表示方法,每一个 node 节点具有(下图):
- 一条指向 Relationships双向链表的指针
- 一条指向 Property 值的的 key-value 链表。
每个 Relation 中有(下图):
- 边 start 节点的 pre 和 next 指针以及
- 边 end 节点的 pre 和 next 指针
- start 与 end 的 id,通过此 id 可以快速定位 node。
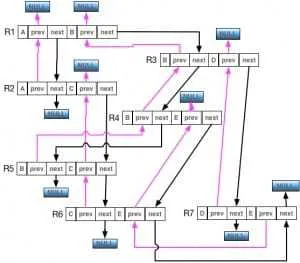
我们可以看出通过这个数据结构,方便的实现如下功能:通过图顶点 Vertex A 遍历他的所有边,找到与他关联的节点的值属性值。
图算法综述
这里我们把常见的图相关的算法分为 3 类,分别为
- 遍历/寻路算法:遍历图的节点与边,求最短路径等
- 中心点算法:衡量图的节点的位置重要性的算法
- 聚类/社区发现算法:对图进行分割、聚类的算法
下面分别介绍一下这些算法与应用场景
遍历寻路
遍历算法是最常见的图算法,
- BFS:广度优先搜索
- 简介:优先遍历所有邻居节点,然后再遍历下一层的邻居。
- 应用:查找邻居,其他算法的基础,如发现最短路径等。对比 DFS 该算法的优点是避免了递归过程。
- DFS:深度优先搜索
- 简介:优先遍历某个邻居节点,并以此不断的深度探索,到达终端节点后再回溯向上遍历其他节点。
- 应用:用于遍历均衡的图 (避免递归太深),以及用在寻找终端结果的算法中,如选择树中叶子胜利还是失败。他也是其他算法的基础。
最短路径算法也是十分普遍的算法
-
单源最短路径:求某个点到其他所有点的最短距离
- 简介:典型算法 Dijkstra,求图中一点到任何点的距离,当然也可以求两点间的最短距离,算法是贪心思想,将节点看为,全部顶点的集合是
,已选集合 , 为未选集合,每次挑选节点加入集合 ,使得到达出发顶点 的距离最小,如此迭代。参考 wiki。 
- 应用:图中两点间的路由算法,如导航,电话网络等
- 简介:典型算法 Dijkstra,求图中一点到任何点的距离,当然也可以求两点间的最短距离,算法是贪心思想,将节点看为,全部顶点的集合是
-
多源最短路径:图中任意两点间的最短距离
- 简介:求图中任意两点的距离,堆典型的就是 Floyd-Warshall 算法,该算法的核心思想是:对于任意节点
, ,如果两个节点的路径最短,必然其最短路径上的其他任意一点 ,有 、 距离都是最短的。具体算法参考 wiki - 应用:评估两组节点间的联通情况。
- 简介:求图中任意两点的距离,堆典型的就是 Floyd-Warshall 算法,该算法的核心思想是:对于任意节点
-
A* 搜索:求两点间的最短距离,某些情况下不能保证最优解
- 简介:启发式寻路算法,相比于 Dijkstra算法,通过引入评估函数
来计算节点 n 的综合距离 ,其中 是节点 n 到源点的实际距离。由此可知,当 为 0 时,即为 Dijkstra。且 h(n) 影响算法的精度和效率,如果保证 评估值不大于真实值时,一定有最优解,单此时效率较低。h(n) 经常使用欧几里得距离、曼哈顿距离等。具体了解可以参考一个 例子 和 wiki - 应用:游戏中求 A 到 B 点的距离,加速了 Dijkstra 的求解
- 简介:启发式寻路算法,相比于 Dijkstra算法,通过引入评估函数
其他
- 最小生成树:求连通图中的极小连通子图
- 简介:Prime 算法,与 Dijkstra 有相似之处,也是贪心思想,全部顶点的集合是
,已选集合 , 为未选集合。核心区别是,在加入已选集合 时,是使得到已选集合 中任意一个顶点的边最小 - 应用:网络设计,如成本最低的路由网络,运输链路等
- 简介:Prime 算法,与 Dijkstra 有相似之处,也是贪心思想,全部顶点的集合是
中心点
这是一类衡量评估某个节点在图中重要性的算法,例如某个点是否是图的中心,是否具有枢纽作用等
- PageRank:通过节点的 PR 值传播来评估节点的重要性
- 简介:流行的网页排序方法,通过传播自身 PR 值给邻居节点,来扩散引用的重要性。最终多次迭代收敛到一个稳定的 PR 值,具有高 PR 值的节点,往往是图中的重要节点。在图中也对应着中心节点
- 应用:网页排序,朋友推荐,生物学中哪些物种的灭绝对其他具有重要影响的评估等,机器学习中提取影响力特征
- 度中心性 Degree Centrality
- 简介:以节点的度的数量衡量节点重要性
- 应用:病毒传播的风险评估,社区中的人气值
- 中介中心性 Betweenness Centrality
- 简介:测量某个节点的最短路径通过数量。即其他两个节点的最短路径通过改节点的次数。该节点一般是 " 桥梁 " 节点,也是核心控制节点
- 应用:瓶颈分析,核心单点分析。社区中信息如何流动的分析
- 接近中心性 Closeness Centrality
- 简介:某节点到其他点距离之和具有最小值,即为中心节点
- 应用:选择公共服务的最优位置,如加油站。社区中传播消息的最佳人选等
聚类与社区发现
可以将这些算法理解为无监督的聚类算法(clustering algorithms)或者分区算法 (partitioning algorithms)
-
LPA:标签传播
- 简介:通过邻居节点的标签中的大多数值(majorities),来推断自己的标签。是一种快速的社区分类算法,适用于大型社区的挖掘。下文会详细介绍。
- 可以用于社区的分类,和半监督学习。如社区中共识的传播
-
寻找强连通图
- 简介:识别出图中强连通子图,使得社区内的节点两两相互连接。
- 应用:识别高密社区,并向亲近此社区的其他用户提供推荐
-
连通图寻找 (弱连通)
- 简介:识别出图中的连通子图,使得社区内的节点可以被连通。直观上,图被分割为 n 个不同的子图。在算法实现层面,可以使用传递消息给邻居节点,消息包含自身见过的最大 vextextId,并保留看过的最大值,如此迭代直到图中没有新的消息传递即可。
- 应用:识别图中断开的地方
-
Louvain Modularity
- 简介:通过 Modularity 来衡量图的聚类质量,并可以生成多层次的社区,具体见下文
- 应用:社交网络等复杂网络的分析,电话联系网络的分析哪些人之间联系密切。欺诈分析等
-
集聚系数:局部集聚系数、整体集聚系数
- 介绍:描述一个图中的顶点之间结集成 团(clique)的程度的系数。两种系数的含义与计算方法如下
- 局部集聚系数:某个顶点,他相邻的顶点组成的子图中,clique(闭合三角) 的数量占总体两两相连的数量的比值。所以,如果邻接节点两两相连,局部集聚系数为 1,如果邻接节点没有任何联系,集聚系数为 0。可以表示为:
,其中,分子为顶点 包含的闭合三角数目,分母为闭合与开放三角数目之和 (也等 k(k-1)/2)
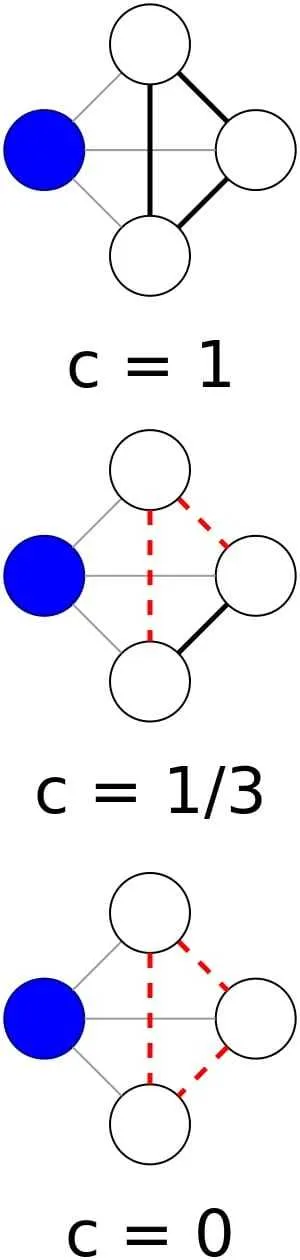
- 整体集聚系数:可以把整个图,看做有 " 闭合三角 " 和 " 开放三角 " 组成的,
表示闭合三角个数, 表示开放三角个数,整体集聚系数可以表示为 。另外,分母值的含义是对图中每个顶点分别对它的邻居两两相连的边的和, ,其中 是每个顶点边的数目。如果用局部集聚系数表示: ,因为 3 个 正好关联了 3 个顶点的闭合三角数目。
- 局部集聚系数:某个顶点,他相邻的顶点组成的子图中,clique(闭合三角) 的数量占总体两两相连的数量的比值。所以,如果邻接节点两两相连,局部集聚系数为 1,如果邻接节点没有任何联系,集聚系数为 0。可以表示为:
- 应用:整体集聚系数可以给出一个图中整体的集聚程度的评估,而局部集聚系数则可以测量图中每一个结点附近的集聚程度。
- 介绍:描述一个图中的顶点之间结集成 团(clique)的程度的系数。两种系数的含义与计算方法如下
-
三角计数与平均集聚系数 (小世界网络)
- 简介:三角计数,表示图中闭合三角的个数。平均集聚系数就是上面所有顶点的局部集聚系数的平均值。
。我们可以对比一下整体集聚系数的公式,他们都是衡量一个图在整体上的集聚程度,但是有一些细微的差别。平均聚集系数为 1,表示图中都是 clique,要求所有节点两两相连,为 0 表示图没有 clique,值约接近 1 约有抱团的趋势。 - 应用:真实世界的网络中一定是部分聚集的,也就是说真实世界的图平均集聚系数会大于随机生成的图。我们把这种真实世界的图叫 "小世界网络"。在这种网络中大部分的节点彼此并不相连,但绝大部分节点之间经过少数几步就可到达。这种网络是一种介于随机和规则之间的图,一般具有较大的平均集聚系数(远大于随机图,小于 1),和较小的平均最短路径长度(logN 成正比)。(最规则的就是完全图,平均最短路径长度=1,平均集聚系数=1)
- 简介:三角计数,表示图中闭合三角的个数。平均集聚系数就是上面所有顶点的局部集聚系数的平均值。
参考文章
分布式图分析
在数据量超过单机容量时,我们会考虑使用分布式图来做数据分析。在分布式场景下,图的表示方法与算法有些许差异,例如,数据如何分布,算法如何并行与同步,此外,还需保证计算的效率,在合理的时间内结果的收敛。下面我们分布从存储与计算角度了解这个问题。
分布式图的存储
图存储的基本方法
大型图的存储总体上有边分割和点分割两种存储方式
- 点分割:每条边只存储一次,只会出现在一台机器上。邻居多的顶点的数据会被复制到多台机器上,
- 优点:可以大幅减少内数据网通信量。
- 缺点:
- 某些增加了存储开销,如边的邻居特别多,则在很多节点上都存储相同的顶点信息
- 每个节点看到的只有部分邻居节点,无法完成这个单点的完整计算,会引发数据同步问题。
- 边分割:每个顶点的数据都存储一次,节点拥有所有邻居节点的引用信息,但有的边会被打断分到两台机器上,邻居的具体数据存储在其他节点
- 优点:
- 可以独立完成该一节点的程序运算
- 节省顶点的存储空间
- 缺点:
- 对图进行基于边的计算时,对于一条两个顶点被分到不同机器上的边来说,要跨机器通信传输数据,内网通信流量大。
- 如果出现某些顶点边很多的情况,会导致数据不均衡
- 优点:
一个例子如下,下图是对 3 条边的图进行分布,a 是使用边分割的方式,节点 ABCD 的节点数据值存储了一份,但是边的数据有 6 份 (还包含节点的引用,虚节点),但是每台机器有节点的完整的边信息。b 是使用了点分割,可以看到 123 条边都只存储了一次,单顶点数据却冗余存储
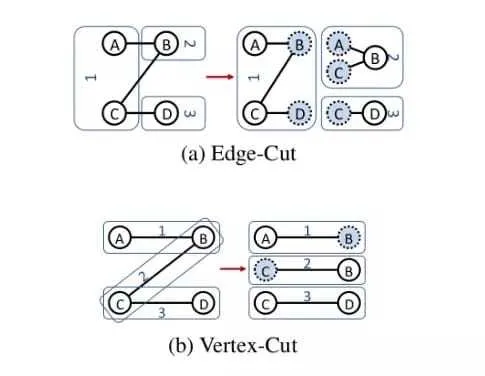
当前主流系统实现均为点分割方式。考虑到不均衡节点在大图中是常见现象,以及磁盘成本的下降,使用冗余的节点存储减少网络通信。
Spark 中的图存储
spark 中图存储的基本方法使用了点分割的方式:每台机器存储 Edge 数据,同时对 Vertex 构建查找路由。Graph 由 EdgeRDD 与 VertexRDD 组成,其中 EdgeRDD 存储了边,包含了 src/dst/边的 attr ;VertexRDD 则含有顶点数据,有 vid 和属性 attr,此外,VertexRDD 还需要能通过顶点定位到所在的边,既即路由功能。下面简要介绍一下 EdgeRDD 与 VertexRDD 的数据结构:
-
EdgeRDD:
- 由 EdgePartition 构成,每个分区内存储了一部分边的数据,边的分布方式由 PartitionStrategy 决定,基本分为三种 EdgePartition2D(使用类似领接矩阵的方式分布边到不同的机器上,保证副本数量不超过
2 * sqrt(numParts));EdgePartition1D(使用 srcid 作为分布);RandomVertexCut(使用 srcid+destid 的 hash 作为分布) - 分区内边按照 srcId 从小到大排序,便于重新组织和使用 array 结构快速访问
- 按排序后的顺序转换外部全局的 id 转化为内部的 localid(0.1.2....数组下标),src 和 dst 都转换 --- 这两者表示方式可以来回转换了
- 构建索引,目的是用 srcid 可以快速找到他的所有边:相同 src 保留第一个 index,index 中记录的是相同 srcId 中第一个出现的 srcId 与其下标。相当于可以用 index 快速在上面 localSrcIds/localDstIds 查找了,再向下找就是它的边
- 边相关的数据 data,也是用本地 id 存储的,单独存在一个数组里
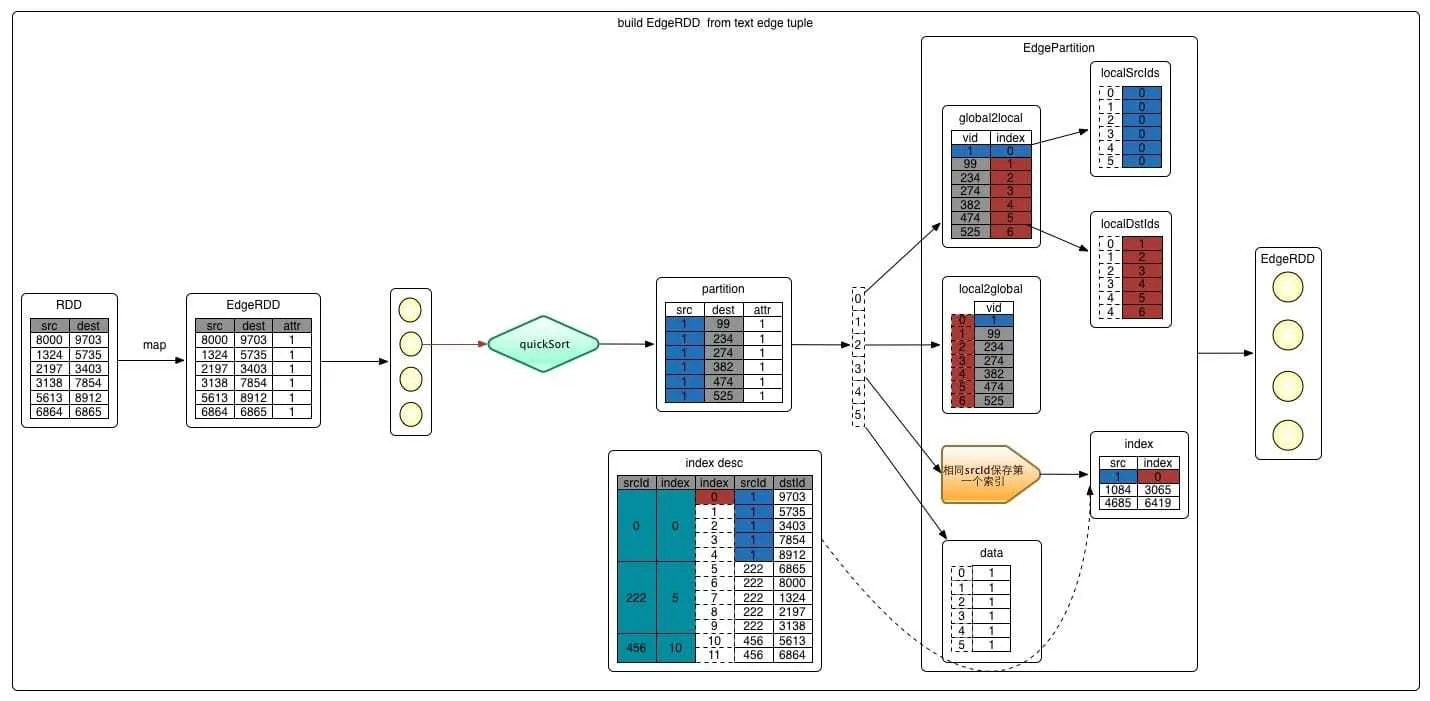
- 由 EdgePartition 构成,每个分区内存储了一部分边的数据,边的分布方式由 PartitionStrategy 决定,基本分为三种 EdgePartition2D(使用类似领接矩阵的方式分布边到不同的机器上,保证副本数量不超过
-
VertexRDD
-
由 vertexPartitions 构成,他的数据是从 EdgeRDD 构建而来,vertexPartitions 存储了顶点的路由表和顶点的属性值,生成过程如下
-
对 Edge 的 partiton 进行 map 操作—>RoutingTableMessage(VertexId, Int) 第二个 Int 包含了关键信息:(边分区 ID--pid,isSrcId/isDstId):作用是以后用这些信息就能找到 VertexId 的边的信息,达到路由的目的!!
-
对 VertexId 进行 shuffle 操作(数目与 edge 分区相同),那么相同的点就到了一个分区
-
对每个点分区构建路由表:可以用点的 (VertexId, Int) 信息快速查找到这个顶点相关的边在哪个 EdgePartiton(通过 pid),见下图的 RoutingTablePartition
-
成 ShippableVertexPartition:构建存储点属性,合并相同重复点的属性 attr 对象,补全缺失的 attr 对象
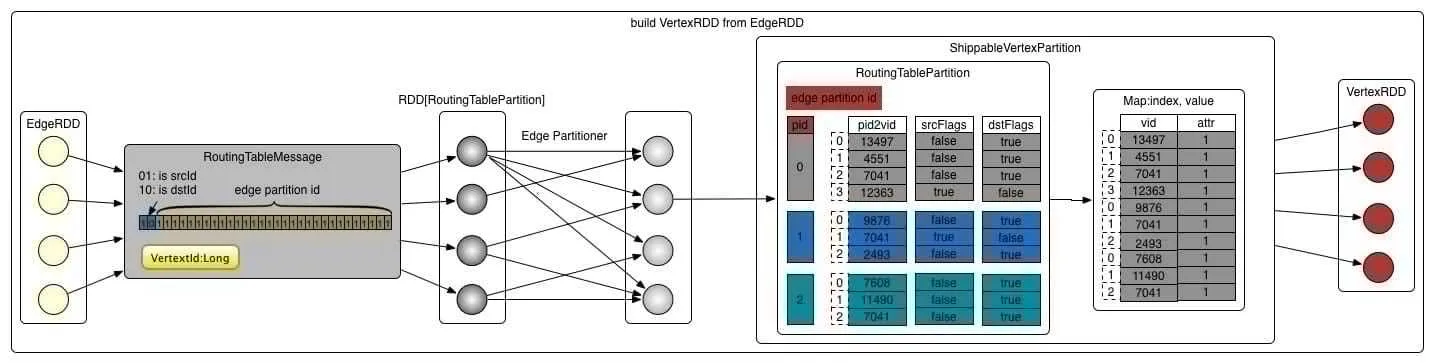
-
分布式图计算模型
图计算的基本思想是 BSP 模型,即 Bulk Synchronous Parallell(分布式批同步),他的基本思想是将图的计算分解成一系列串行的 superstep(超步):
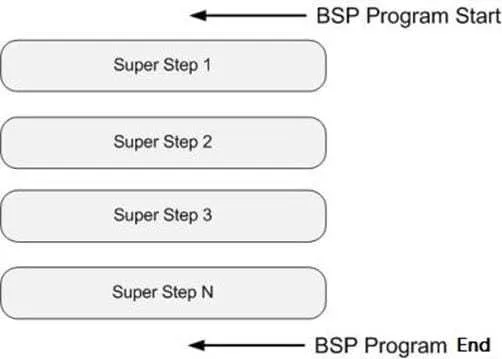
每一个超步内部强调计算与通讯分离,具体而言包含三个阶段:
- 并行计算 (local computation):在本地进行计算,无外部的数据访问
- 全局通信 (非本地数据通信):发送数据给其他节点
- 栅栏同步 (等待通信行为结束):同步阶段,等待所有节点都接收到数据
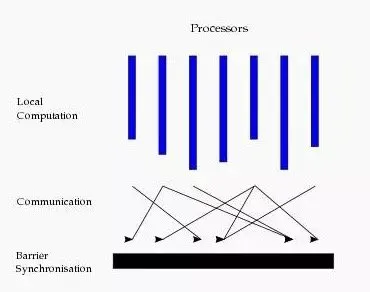
我们发现上述模型也有类似与 shuffle 的过程,但是对比 MR,BSP 模型具有下列不同:
- MR 是一个数据流模型,任务 shuffle 产出的数据发送给了其他新的任务 (reduce 任务),并且伴随着数据落盘等操作,而 BSP 中任务是没有变。
- MR 需要多个 job,即多轮启动任务才能完成上述算法的多个超步计算,而 BSP 中是一个 job
- 除此之外,由于 BSP 对消息的路由是固定,往往可以做很多优化
BSP 模型的传统实现
BSP 的有两种常见的计算框架:
- Pregel 框架:该实现中以 " 顶点 " 为中心,对顶点应用函数进行计算并且顶点的值可以修改。而边没有任何计算与修改。
-
在每个 superstep 中,每个顶点具有 active 和 inactive 两个状态。收到消息后就会变为 active 状态,并执行用户定义的同一个函数。这个函数可以对其他邻接边发出 msg,修改自身的值,或者判断满足某些条件后把顶点人工 halt 为 inactive
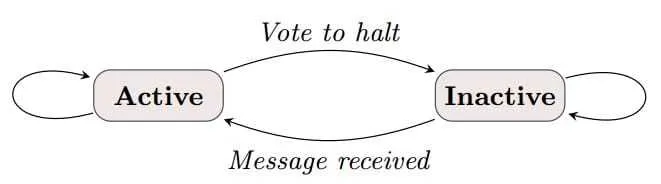
-
当系统中没有消息再 active 节点时,所有节点都是 inactive 状态,算法迭代终止
-
主要缺点:如果遇到某个节点有众多的边,会导致数据不均衡,某个节点运行时间过长。降低了算法的并发性。ps:非常类似于边分割存储的问题!
-
- GraphLab 框架:该算法以点分割为基础,一个顶点的多个边被存储到不同的机器上,解决数据不均衡问题。此时我们需要汇总顶点相关边的计算。因此,一台机器作为
master顶点,其余机器作为mirror。一台机器内部相当于有一个 " 本地图 ",使用多个线程分摊进程中所有顶点的操作。每个顶点的操作包括gather->apply->scatter-
gather:顶点从本地收集相连的边的数据,对顶点、边都是只读的
-
apply:
mirror将gather阶段计算的结果发送给master顶点,master进行汇总并结合上一步的顶点数据,按照业务需求进行进一步的计算,然后更新master的顶点数据,并同步给mirror。Apply阶段中,工作顶点可修改,边不可修改。 -
scatter:顶点更新完成之后,更新边上的数据,并通知对其有依赖的邻结顶点更新状态。在
scatter过程中,工作顶点只读,边上数据可写。(对比 Pregel,注意这里边的数据可以修改) -
存储结构如下:
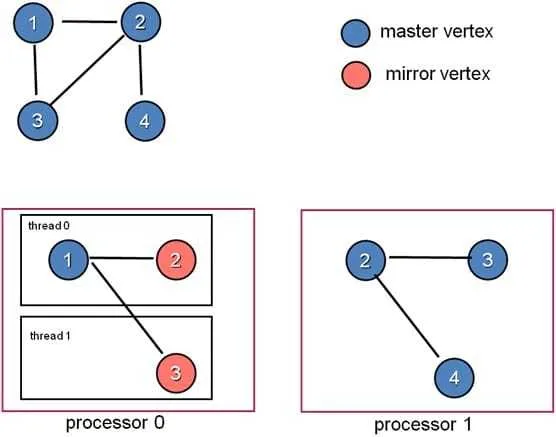
-
计算过程如下:
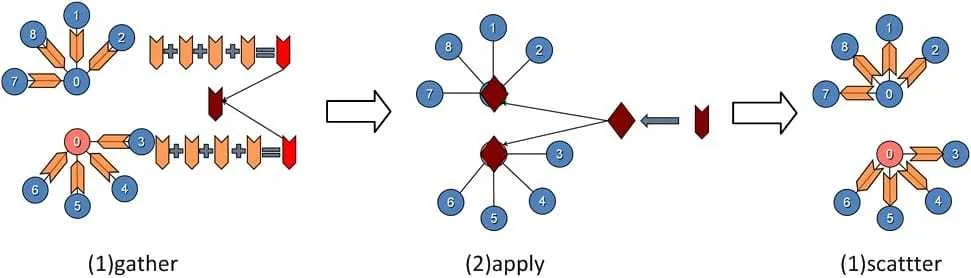
-
下面是分别使用 Pregel 框架和 GraphLab 框架实现 pagerank 的伪代码:
// Pregel框架实现pagerank,被图的顶点调用
def PageRank(v: Id, msgs: List[Double]) {
// 计算消息和
var msgSum = 0
for (m <- msgs) { msgSum = msgSum + m }
// 更新 PageRank (PR)
A(v).PR = 0.15 + 0.85 * msgSum
// 广播新的PR消息
for (j <- OutNbrs(v)) {
msg = A(v).PR / A(v).NumLinks
send_msg(to=j, msg)
}
// 检查终止
if (converged(A(v).PR)) voteToHalt(v)
}
// GraphLab框架实现pagerank
// gather汇总,被图的边调用
def Gather(a: Double, b: Double) = a + b
// apply更新顶点,图的顶点调用(msg是数据交换了)
def Apply(v, msgSum) {
A(v).PR = 0.15 + 0.85 * msgSum
if (converged(A(v).PR)) voteToHalt(v)
}
// scatter更新边
def Scatter(v, j) = A(v).PR / A(v).NumLinks
Spark Graphx 中 BSP 模型的实现
GraphX 也是基于 BSP 模式。GraphX 的核心 API 是 aggregateMessages,此外基于次 API 还封装了一个 类似Pregel的操作,它结合了的 Pregel 和 GraphLab 框架的特点。我们可以**把 Spark 中的 Pregel 理解为多轮的 aggregateMessages + joinVertices 的组合(即一个 superstep)。**首先我们看一下 aggregateMessages API:
// api定义
class Graph[VD, ED] {
def aggregateMessages[Msg: ClassTag](
sendMsg: EdgeContext[VD, ED, Msg] => Unit,
mergeMsg: (Msg, Msg) => Msg,
tripletFields: TripletFields = TripletFields.All)
: VertexRDD[Msg]
def joinVertices[U](table: RDD[(VertexId, U)])(mapFunc: (VertexId, VD, U) => VD): Graph[VD, ED]
}
aggregateMessages 计算过程:先遍历边,再遍历顶点(只遍历 send 后的顶点),最终形成(vid,msg)的 RDD,VertexRDD[Msg]
- sendMsg:类比 map,遍历图的边(triplet),调用你提供的 sendMsg,在里面你可以通过 EdgeContext 发送 Msg 给 Src 还是 Dst
- mergeMsg:类比 Reduce,每个 Send 目标节点都会调用此函数,合并 Send 过来的 Msg
- tripletFields:EdgeContext 的访问权限控制,为内部提供优化,比如在上面的函数中只用 src 点的属性,TripletFields.Src
- 返回的是 VertexRDD[Msg],是一个顶点的 RDD,里面是 send 的消息,没有 Msg 的顶点就不会返回
- Vertices that did not receive a message are not included in the returned VertexRDD
joinVertices 操作则是把原来的 graph 与收到的 msg 关联起来,并定义了顶点的更新函数 mapFunc`
// 关联消息的操作,vprog是顶点更新
g = g.joinVertices(messages)(vprog)
具体实现参考 Graphx 的 Pregel源码。
对比:Graphx 中的
Pregel与原始的 Pregel 框架和 GraphLab 有什么异同?
- 我们可以发现,这里的 Pregel 借鉴了 GraphLab 的思想,还是以点分割为为基础,第一步先遍历边,依据边 sendmsg,最终 joinVectices,这里相当于 gather 与 apply 的过程了。
- 但是,这里并没有对边的修改,可以认为是 Pregel 模型
部分图算法的分布式实现举例
我们使用前面介绍的 Graphx 的 Pregel 方法来实现图算法,这里举两个源码中的例子,分别是 PageRank 和 LPA,可以发现使用该方法,对于这两种迭代算法的实现都十分简短
一个 Graphx 版本的 PageRank 实现如下:
val pagerankGraph: Graph[Double, Double] = graph
// Associate the degree with each vertex
.outerJoinVertices(graph.outDegrees) {
(vid, vdata, deg) => deg.getOrElse(0)
}
// Set the weight on the edges based on the degree
.mapTriplets(e => 1.0 / e.srcAttr)
// Set the vertex attributes to the initial pagerank values
.mapVertices((id, attr) => 1.0)
def vertexProgram(id: VertexId, attr: Double, msgSum: Double): Double =
resetProb + (1.0 - resetProb) * msgSum
def sendMessage(id: VertexId, edge: EdgeTriplet[Double, Double]): Iterator[(VertexId, Double)] =
Iterator((edge.dstId, edge.srcAttr * edge.attr))
def messageCombiner(a: Double, b: Double): Double = a + b
val initialMessage = 0.0
// Execute Pregel for a fixed number of iterations.
Pregel(pagerankGraph, initialMessage, numIter)(
vertexProgram, sendMessage, messageCombiner)
}}}
一个 Graphx 版本的 LPA 实现如下(源码文件):
val lpaGraph = graph.mapVertices { case (vid, _) => vid }
// 发送自己的标签给邻居,使用顶点id作为标签
def sendMessage(e: EdgeTriplet[VertexId, ED]): Iterator[(VertexId, Map[VertexId, Long])] = {
Iterator((e.srcId, Map(e.dstAttr -> 1L)), (e.dstId, Map(e.srcAttr -> 1L)))
}
// 统计邻居节点标签的数量
def mergeMessage(count1: Map[VertexId, Long], count2: Map[VertexId, Long])
: Map[VertexId, Long] = {
val map = mutable.Map[VertexId, Long]()
(count1.keySet ++ count2.keySet).foreach { i =>
val count1Val = count1.getOrElse(i, 0L)
val count2Val = count2.getOrElse(i, 0L)
map.put(i, count1Val + count2Val)
}
map
}
// 使用数量最多的邻居标签作为顶点的属性值
def vertexProgram(vid: VertexId, attr: Long, message: Map[VertexId, Long]): VertexId = {
if (message.isEmpty) attr else message.maxBy(_._2)._1
}
val initialMessage = Map[VertexId, Long]()
// 迭代计算
Pregel(lpaGraph, initialMessage, maxIterations = maxSteps)(
vprog = vertexProgram,
sendMsg = sendMessage,
mergeMsg = mergeMessage)
}
社区发现算法
社区发现是什么
首先,我们需要解释在图场景下社区的概念。社区是在图中具有如下特征的子图:
- 社区内部,顶点相对接近/密集
- 不同社区之间,顶点相对疏远/稀疏
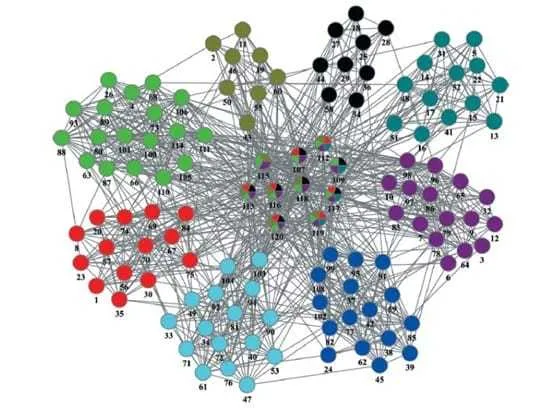
从上述定义可以看出:社区是一个比较含糊的概念,只给出了一个定性的刻画。
我们可以把社区发现算法对比与无监督学习中的聚类算法,典型的如 K-means 系列算法,他们也是把相邻的节点进行聚合分类,不同的只有 k-means 中通过特征的『距离』作为衡量的标准。图的社区发现中通过边以及边的权重作为依据。
社区发现算法系列
算法分类
社区发现中,我们希望把一个图分割成 N 个互不相交的社区(N 往往未知),一般有两种思路:第一种是 cut,也就是划分,把无关联的边去掉,进而取到核心的社区。第二种是 gather,也就是聚合,将关联性比较大的顶点聚集起来,关联性较小的顶点剔除出去。
其中 cut 算法的典型代表是:k-core decomposition。基本思想是对图中的所有顶点进行判定,若度小于 K,则将该点和所有关联的边从图中删除,然后再进行下一轮迭代,直到图中所有的顶的度都大于 K。
LOOP
(1)找到小于 K 的点
(2)删除步骤 1 找到的点和边
(3)继续进行步骤 1,若找不到符合条件的点则结束
END
gather 算法的典型代表是:Label Propagation Algorithm 标签传播算法,每个顶点在开始的时候都设立自己的标签,然后向所有的邻居进行广播。每个顶点在接收到广播的时候呢,将收到的最多的标签作为自己的标签,进行下一轮的迭代。
初始化: (1)顶点标签
LOOP
(2)发送自己的标签
(3)接收标签
(4)将最大标签作为自己的标签
(5)继续进行方法 2,直到达到最大迭代次数。
END
效果评估 -Modularity
不同算法的效果如何衡量,即社区质量评估是社区发现中的一个重要问题,一般我们使用一个数值标量来做为评估标准:Modularity。定义如下:网络中连接社区结构内部顶点的边所占的比例与另外一个随机网络中连接社区结构内部顶点的边所占比例的期望值相减得到的差值。
Modularity 的定义历史可以参考 这篇文章。重点理解:
- 从不同角度看 modularity 公式,1. 顶点角度(2006 论文)2.社区角度(2004 论文)
- 两者的等价关系
常见算法
除了我们之前提到的 k-core decomposition 与 LPA 外,有一系列基于他们衍生算法,主要解决算法中存在的问题。这里我们讨论一下 LPA 的衍生算法。在 LPA 算法中,只能将顶点划分一个社区内,这样会导致一个经常出现的顶点的分类结果震荡问题。最常见的改进是 SLPA 算法(Speaker Listener Label Label Propagation Algorithm),SLPA 中引入了 Listener 和 Speaker 两个比较形象的概念,你可以这么来理解:在刷新节点标签的过程中,任意选取一个节点作为 listener,则其所有邻居节点就是它的 speaker 了,speaker 通常不止一个,一大群 speaker 在七嘴八舌时,listener 到底该听谁的呢?这时我们就需要制定一个规则。在 LPA 中,我们以出现次数最多的标签来做决断,其实这就是一种规则。只不过在 SLPA 框架里,规则的选取比较多罢了(可以由用户指定)。当然,与 LPA 相比,SLPA 最大的特点在于:它会记录每一个节点在刷新迭代过程中的历史标签序列(例如迭代 T 次,则每个节点将保存一个长度为 T 的序列,如上图所示),当迭代停止后,对每一个节点历史标签序列中各(互异)标签出现的频率做统计,按照某一给定的阀值过滤掉那些出现频率小的标签,剩下的即为该节点的标签(通常有多个)。过程如下:
初始化:(1)顶点标签
LOOP
(2)根据**规则**发送标签
(3)接收标签,将标签以一定的**规则**追加到自己的标签中
(4)继续进行方法 2,直到达到最大迭代次数。
END
(5)对结果进行解析,自行决定单顶点社区的个数。
此外,还有一些衍生算法致力于解决 LPA 中的大社区问题,即分类中会出现某些社区具有特别巨量的节点。我们往往通过引入传播距离作为控制,改进算法的结果,常见的算法有 HANP,DCLP 等,可以参考 这篇文章。
另一大类的社区算法还会在算法运行过程中使用 Modularity 作为优化目标来进一步指导节点的分类,这就是我们最后会详细说明的 Fast unfolding Louvain 算法,该算法除了分类效果最好外,还可以生成多分辨率图,巧妙的避免了『巨型社区』的问题。
总结常见的社区发现算法如下:
- Cut 算法
- k-core decomposition
- Gather 算法
- LPA 以及衍生优化
- SLPA - Speaker Listener Label Label Propagation Algorithm - 重叠社区 解决震荡
- HANP:传播距离解决巨型社区问题
- DCLP
- AM-DCLP
- SDCLP
- 使用 Modularity 作为目标
- Fast unfolding Louvain 算法
- LPA 以及衍生优化
社区发现算法实现 -Louvain 实现
当前效果比较好的社区发现算法是 Fast unfolding Louvain 算法。该算法对于大数据量的图(亿节点 +)具有快速的聚类效果,此外,通过多分辨率图的方式解决『大社区』问题。可以阅读论文:fast unfolding of communities in large networks,这篇论文十分紧凑推荐阅读。
- 基本思想:贪心算法,优化图的总体 modularity 值
- 算法过程:两 step 构成一个 pass,每个 pass 都会形成一个社区,迭代 n 次 pass,形成 n 个分层的社区(论文中叫不同分辨率的社区)
- step1,给每个点分配社区 id,遍历所有顶点,计算他的邻接节点,查看是否『移动当前社区到邻居社区对整体 modularity 值』的影响,这里涉及一个重要公式,来快速计算 modularity 变化量(delta),重复到整个图模度收敛为止(modularity 变化为 0),注意:这个过程可能对某些顶点重复考察
- step2,合并上面的每一个社区为一个新顶点。合并过程中,对于原图内部的 N 条边,在新节点处加入 N 条 self-loop 边
- loop 上述步骤
- 优点
- 快,使得瓶颈在存储而不是计算,论文中点击能跑上亿个节点。维基百科 中时间复杂度 O(nlogn)
- 结果分层结构,解决其他 modularity 算法对小社区识别度的问题(偏向于识别大社区)
- 缺点
- 可解释性:各层的含义还是得自己摸索,尤其是中间层
DGA 库介绍与源码
背景:实际开发中并没有重头开发算法库,而是在第一版本中使用了第三方的库,这个库在 github 上使用的人非常少,风险很高
文档:http://sotera.github.io/distributed-graph-analytics/
介绍:这个库主要是在 Hadoop 环境 (Giraph) 和 Spark 环境 (GraphX) 下实现了一些图的算法。这些框架都使用了 BSP 模型(同步栅栏模型).
DGA 实现了如下 5 种算法:
- High Betweenness Set Extraction
- Weakly Connected Components
- Page Rank
- Leaf Compression
- Louvain Modularity(beta 版本,大量的 bug)
Louvain Modularity 算法源码分析与导读
文档资料
- Louvain算法文档介绍:比较简单没什么内容(看一下
minimum.progressprogress.tries参数的设置),主要看看源码com.soteradefense.dga.graphx - Louvain算法运行方法
代码流程分析
- 从上面运行方法入口 DGARunner 类:
- 主要构造了数据集自定义的
EdgeInputFormat格式,src dst weight initialGraph=EdgeInputFormat.getGraphFromStringEdgeList其实就是生成了一个边的图runner = new HDFSLouvainRunner(minProgress, progressCounter, outputPath)Louvain 算法的入口类runner.run(sparkContext, initialGraph)传入图开始运行
- 主要构造了数据集自定义的
- HDFSLouvainRunner 是真正开始运行的地方,其实他的主要方法是他父类
AbstractLouvainRunner的run- 构造算法核心的类:
LouvainCore var louvainGraph = louvainCore.createLouvainGraph(graph)构造图- 循环,一个 pass 如下:
louvainCore.louvain(sc, louvainGraph, minimumCompressionProgress, progressCounter)louvainGraph = louvainCore.compressGraph(louvainGraph)
- 构造算法核心的类:
louvain 迭代过程分析:
louvainCore.louvain(sc, louvainGraph, minimumCompressionProgress, progressCounter),输入 louvainGraph
- 计算 totalGraphWeight,(这里是图的边的权重 *2,或者叫度的权重)
- 使用 aggregateMessages,将每个 vertex 的附近的邻居的社区 id 和 communitySigmaTot 拿到
- sendCommunityData:迭代边,发送(community,communitySigmaTot)到两侧
- mergeCommunityMessages:合并成 map(community->communitySigmaTot): 合并效率问题
- do-while 迭代:注意终止条件:stop-- 含义表示 update<minProgress 的进展太小 (合并节点太少)
- even 条件:为了防止死锁(什么情况下?一个顶点一会分给 A 社区,一会 B 社区,来回循环?)-- 每次迭代只修改图中一半的顶点: only allow changes from low to high communties on even cyces and high to low on odd cycles
- louvainVertJoin:核心函数,遍历顶点,对之前的 map 中的每个邻居进行 deltaQ 计算,选择最大的,把当前节点划入该社区,调用了
q函数进行计算。 - communityUpdate: 重新计算新社区的 total weigh(CommunitySigmatTot)使用 nodeWeight (因为上面重新分配了社区)
- 分配 CommunitySigmatTot 新值给所有节点
- 最终更新 louvainGraph
- 使用 aggregateMessages 计算(同上面 2)
- 计算终止条件:update 数目(更新的/change 的节点数目)
- 计算最终的 actualQ(modularity)返回:算法就是先用公式算每个社区的 modularity,然后整体求和
可能优化点:aggregateMessages 不用 map,而是直接算 deltaQ 并取最大值
deltaQ 的计算问题
我们发现算法实现时的 deltaQ 计算与原始论文不同。由于我们只需要比较 deltaQ 值的相对大小,因此上述两个公式是等价的。证明可以参考 这篇文章。
重点理解:我们只需要计算相对大小即可(就可以比较找出最大变换),因此在 unfold fast 论文中 deltaQ 计算公式:
为了简化计算,可以转变为相对值:
DGA 实现中的 deltaQ 问题的理解:
论文中理解 deltaQ 的关键点是:首先假设某个节点在图中在一个独立的社区中,然后有 deltaQ 的公式:
这个公式中的,最后一项就是基于前面的假设,即这个节点是个独立的社区,所以他自身的 modularity 是
。 但是,注意但是!如果节点不在一个独立的社区中,怎么办?论文的方案很简单:把这个过程分为两步,第一步把节点从原来的社区移走,第二步再把节点加入新社区。这里的第一步就是上面的公式的负数。如果算法实现没错的化,就是只移动节点到有增加 deltQ 的社区,那么移出一定是个负数,因此,最后完整的我们需要看看这个第一步的 deltaQ 的负数和第二步 deltaQ 的正数之和是不是>0。
但是,但是。。实际实现算法的时候没有这么干!!
上面我们说为了简化计算,deltaQ 可以转变为相对值:在 DGA 库中,我们遍历每个节点,我们尝试把当前节点加入到他邻居的社区(注意表述的顺序,谁加入到谁)。因此,如果这个节点他不是一个单独的社区,他必然要先脱离自己原来的社区,对每个节点而言这是一个固定的值(一个节点比如划分到某个社区了!)。因此我们在寻找『最大 deltaQ 的相邻节点社区』的过程中,只需要比较相对值,可以忽略这个固定的值。。。。
但是,正如上一段所述,如何保证这个两步之和大于 0 呢?这就需要在扫描相邻社区时,『特殊』处理,如果发现相邻社区与节点自己的社区相同时,不跳过!!(我们可能误认为加入相同社区 deltaQ=0)照常计算 deltaQ,但是 $\sum_{t o t} $ 中需要减去该节点自身的值,然后算出 deltaQ。把这个 deltaQ 和其他 deltaQ 一起参与到最终的『最大 deltaQ 的相邻节点社区』选举中。如果加入其他社区没有收益,就会导致这个『特殊』的 deltaQ 脱颖而出。(隐含我们不需要对 deltaQ>0 进行判断,但是 lib 中还是判断了)
多层图的 Modularity/图压缩算法理解
论文在阶段二中有个重要的点:如何压缩图,具体而言每个社区是一个新顶点,如何处理原来的社区内关系?
- 论文中的方法是:对社区内部的部边(不与社区外相连的边)最为self-loop 边(就是新顶点自己连到自己的边,在邻接矩阵的表示中就是对角线!)。这么处理有个非常大的好处,对于压缩后的图,前面的 modularity,deltaQ 的计算公式与结果不会改变。
- 在 DGA 库中的实现方法是,使用新节点的 internalWeight 值(含义与上面 Louvain 类似),后续计算 modularity 和 deltaQ 的时候需要考虑这个值
理解:图的压缩不影响 Modularity 的值
我们在 compressGraph 图之后,此时同一个社区的多个节点会合并成一个 1 个节点,并根据社区内连接到数量 N 相应的增加 N 个 self-loop 连接(在 DGA 中使用 internalWeight 表示)。
注意:压缩后的图的 Modularity 与压缩前的 Modularity 相等!!!,使用的公式相同:再次理解这个公式:
图中相同社区内有连接的节点间的边 weight 值和 这个是一个社区内所有的节点的度的两两乘积(不管有没有边相连,只要属于一个社区就行)
DGA 库优化与 Bug 分析
在使用此库时,发现了大量的问题(并且 test case 无法通过),最终使得 Louvain 算法的实现完全错误,导致大量情况下提前结束迭代,此时算法并未收敛。除了错误外,还有大量的性能问题,总结三类问题如下:
- 对 Spark 的误用,导致算法实现错误,提前收敛
- 对 Louvain 算法论文理解的偏差,导致部分边缘节点分类错误
- 代码性能性能问题,导致关键部分运行极慢
Spark 误用时导致的 Bug:
- rdd 内 map 函数重复计算多次。原因:没有 cache(或者 unpersist)的 rdd 会有这种现象
- unpersist 过早的问题:如果在正在触发计算之前 unpersist 会导致 cache 的效果没有(lazy),如下
val rdd=sc.read(xxx).cache
val rdd2=rdd.map(x=>x+1)
val rdd3=rdd.map(x=>x+1)
rdd.unpersist() // 无效代码
rdd2.count rdd3.count
// 应当在这里!!
rdd.unpersist()
- rdd 是不可变数据集!!,一般情况下 RDD[CustomObj] 对象都是 case class 定义的,但是,代码中奇葩的使用了 class 定义 (即
LouvainData类),并定义了内部的 var 变量,在 map,join 等中直接修改变量。导致结果玄学,没有意义。
val rdd:RDD[CustomObj]=sc.read(xxx)
val rdd2=rdd.map(d=>d.flag=1) // 不可以直接修改,而是应该返回新对象!!!
rdd2.filter(d.flag==1)
innerJoin误用,在计算最终的 actualQ 值时原始代码中使用了 GraphX API 的innerJoin函数,该函数只会返回两个 RDD 中都存在的 join key。丢弃左侧 RDD 中存在,但是右侧 RDD 不存在的 Key,因此最终计算的整个图的 modularity 值缺失了大量的图的值(具体到算法中丢弃了那些没有在本层迭代中发生 modularity 变化的社区),正确算法应该使用leftJoin
deltaQ 计算公式错误:
算法实现中 q 函数的计算公式是 deltaQ = k_i_in - (k_i * sigma_tot / M),但是,这的 M 的含义是 edge_weight*2,原始公式中对应的是 edge_weight 之和,这里的 M 应该替换为 M/2
Scala 代码性能问题:
性能问题主要发生在 GraphX 中最重要的 API:aggregateMessages 中。在原始算法中代码如下:
private def sendCommunityData(e: EdgeContext[LouvainData, Long, Map[(Long, Long), Long]]) = {
val m1 = (Map((e.srcAttr.community, e.srcAttr.communitySigmaTot) -> e.attr))
val m2 = (Map((e.dstAttr.community, e.dstAttr.communitySigmaTot) -> e.attr))
e.sendToSrc(m2)
e.sendToDst(m1)
}
/**
* Merge neighborhood community data into a single message for each vertex
*/
private def mergeCommunityMessages(m1: Map[(Long, Long), Long], m2: Map[(Long, Long), Long]) = {
val newMap = scala.collection.mutable.HashMap[(Long, Long), Long]()
m1.foreach({ case (k, v) =>
if (newMap.contains(k)) newMap(k) = newMap(k) + v
else newMap(k) = v
})
m2.foreach({ case (k, v) =>
if (newMap.contains(k)) newMap(k) = newMap(k) + v
else newMap(k) = v
})
newMap.toMap
}
// 调用
communityRDD = louvainGraph.aggregateMessages(sendCommunityData, mergeCommunityMessages)
核心问题发生在 mergeCommunityMessages 函数的 newMap.toMap 中,在 scala 的实现中,这里会新创建大量的对象,导致 GC 严重,拖慢了整个算法。改进方法如下:
private def mergeCommunityMessages(m1: Map[(Long, Long), Long], m2: Map[(Long, Long), Long]) = {
val merged = (m2 foldLeft m1) (
(acc, v) => acc + (v._1 -> (v._2 + acc.getOrElse(v._1, 0L)))
)
merged
}
由于该函数被大量调用,此优化带来性能 5x 以上的提升。
Louvain 算法应用思考
- 非对等节点构建图,容易导致被某些大节点吸附,典型的就是大的 query 下面集合了一堆 uid,解决方案就是合理分配连线的 weigh
- 该算法只是一个聚类算法,只能提供结构特性,
- 异常结构。如高密度节点,但是有可能只是正常的特征,如热门搜索词
- 使用标签数据 -- 典型的用作弊率来标识异常社区
- 使用异常检测 -- 如使用多元高斯分布
- 在构建多层图时,整体图的 Modularity 应当会收敛到一个值(从 0--1)
尾巴:使用 Gephi 可视化图分析
图可视化方法是我们在开发测试和效果验证的重要手段,调研如下,对于巨型图(百万节点)的可视化问题(也叫多分辨率显示)没有太好的现成工具。下面是一些少量顶点的图可视化工具,其中最最常见的,也是在图的论文中广泛使用来展示实验效果的工具就是 gephi。
-
gephi:最常用工具,跨平台
- 优点:图形操作界面,用的人多很多教程,自带很多算法,基本很多图算法论文都用他来画图
- 缺点:数据量支持少,10000 以内节点可视化
-
graph-tool:一个 py 的库
- 优点:c++ 实现,高效,据说几十万没问题,可以当库用
- 缺点:没用过,待测试
-
- 优点:云平台 gpu 渲染,用 d3 显示,几百万节点没问题,可以在 notebook 里面直接用(py 库)
- 缺点:在线工具,要联网
-
其他有论文将 multi resolution 的方案来显示大规模图(使用分层的 tree 架构展现图,类似 googleearch?),但是没找到现成的软件
使用 Gephi 来运行 louvain 算法的简单可视化教程如下:
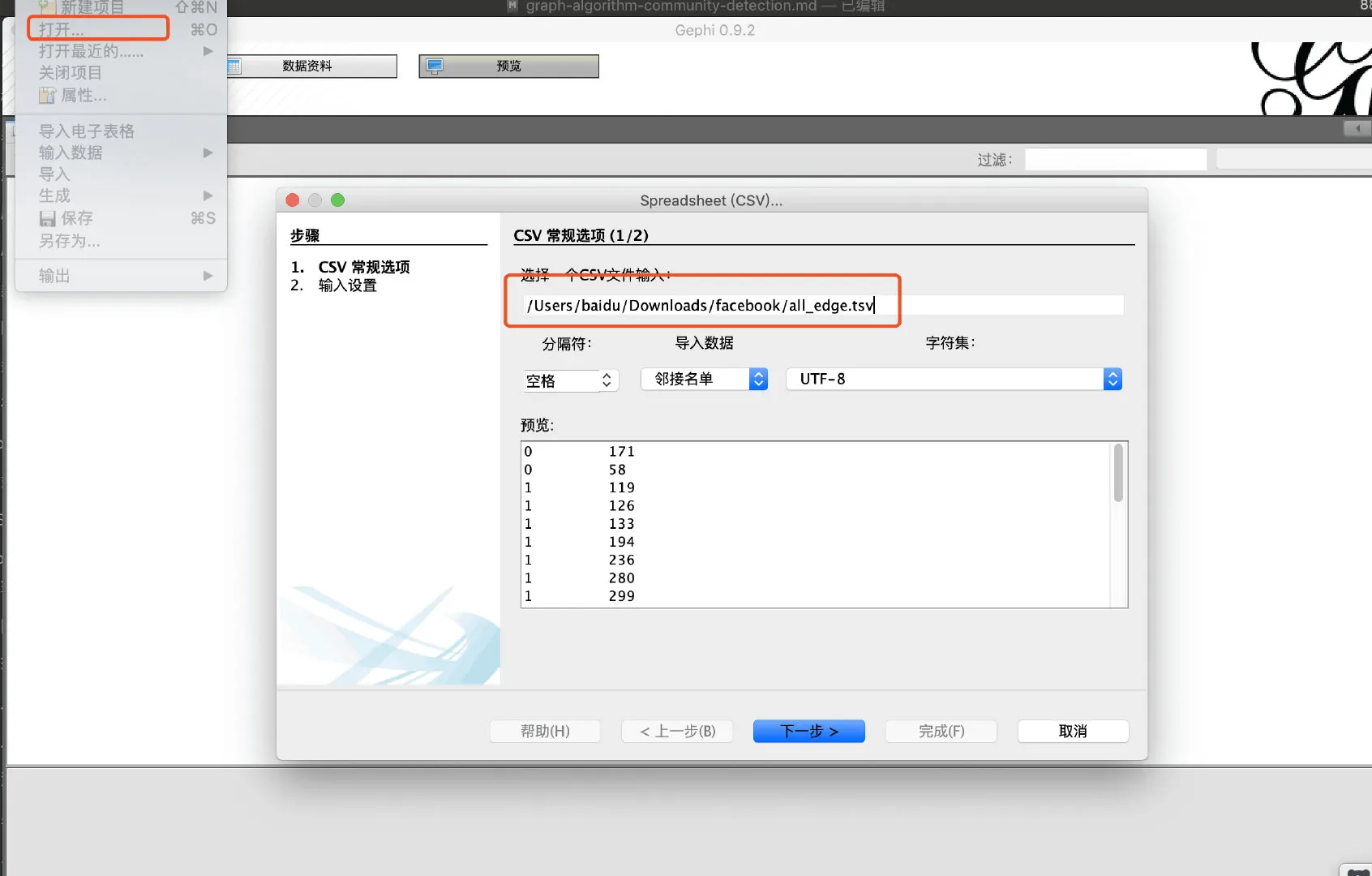
- 导入数据,数据格式,为 tsv,即 tab 分隔的边
- 点击右侧,模块化的运行按钮启动运行算法
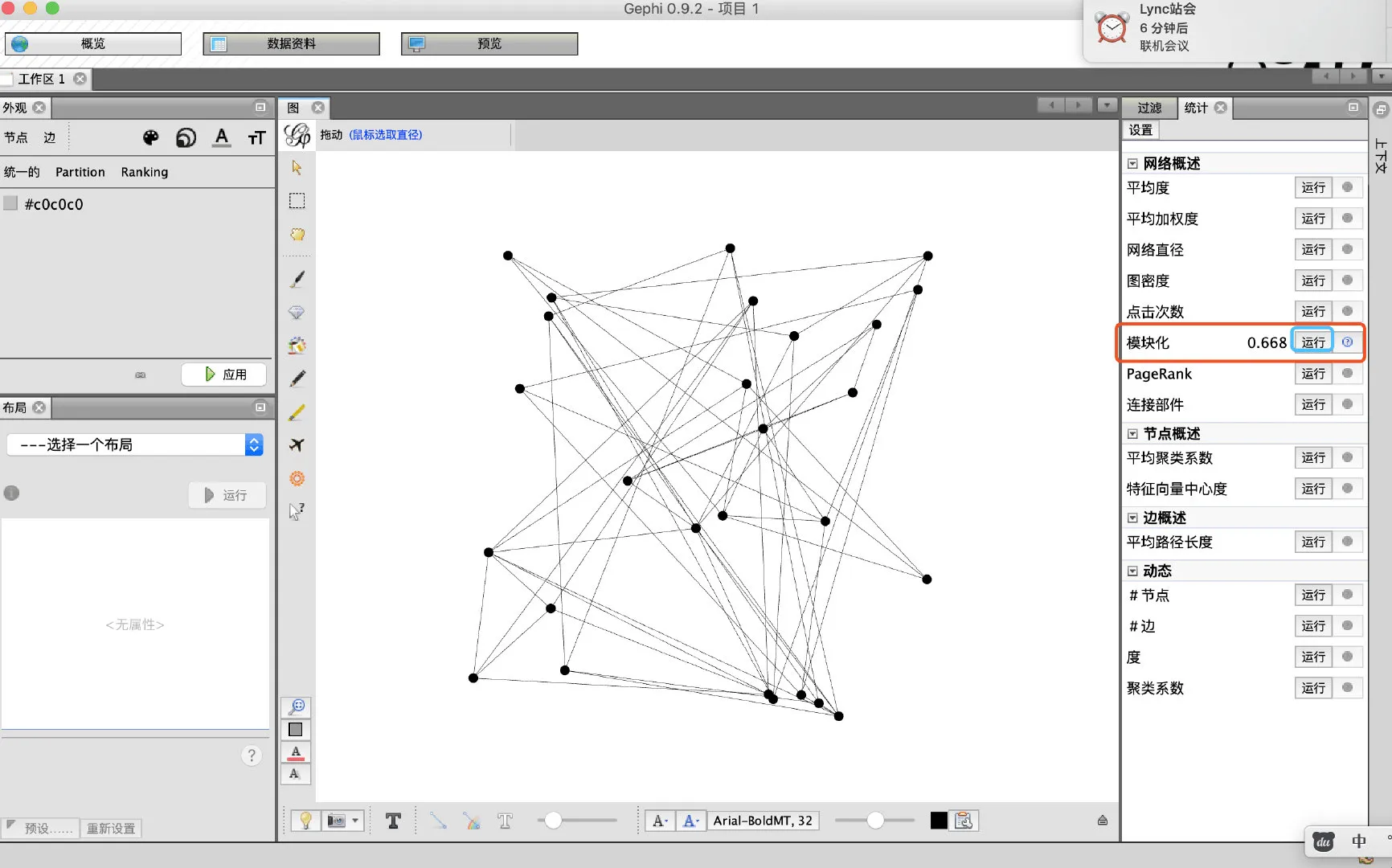
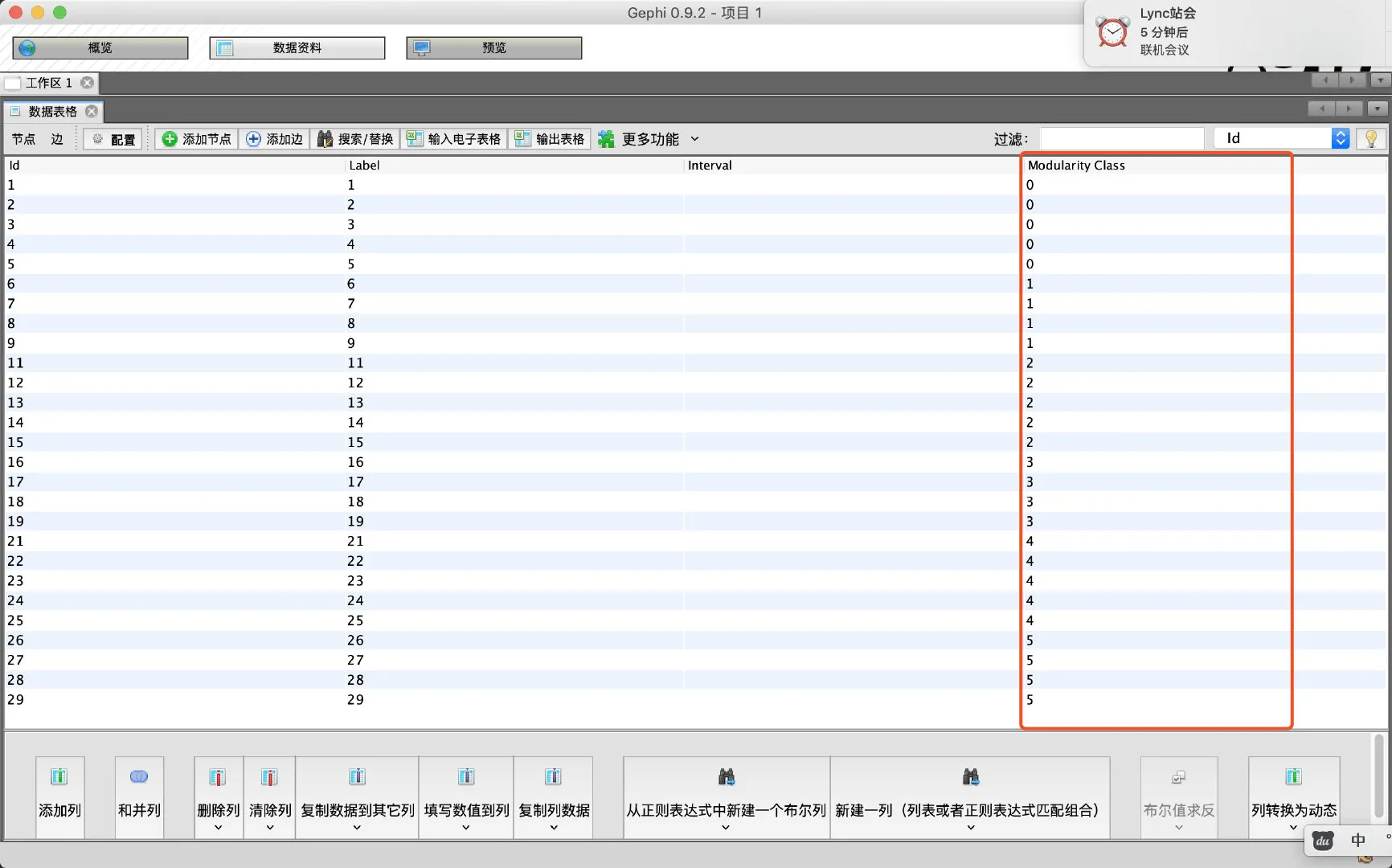
- 此时在数据页面出现新的一列,表示分类结果
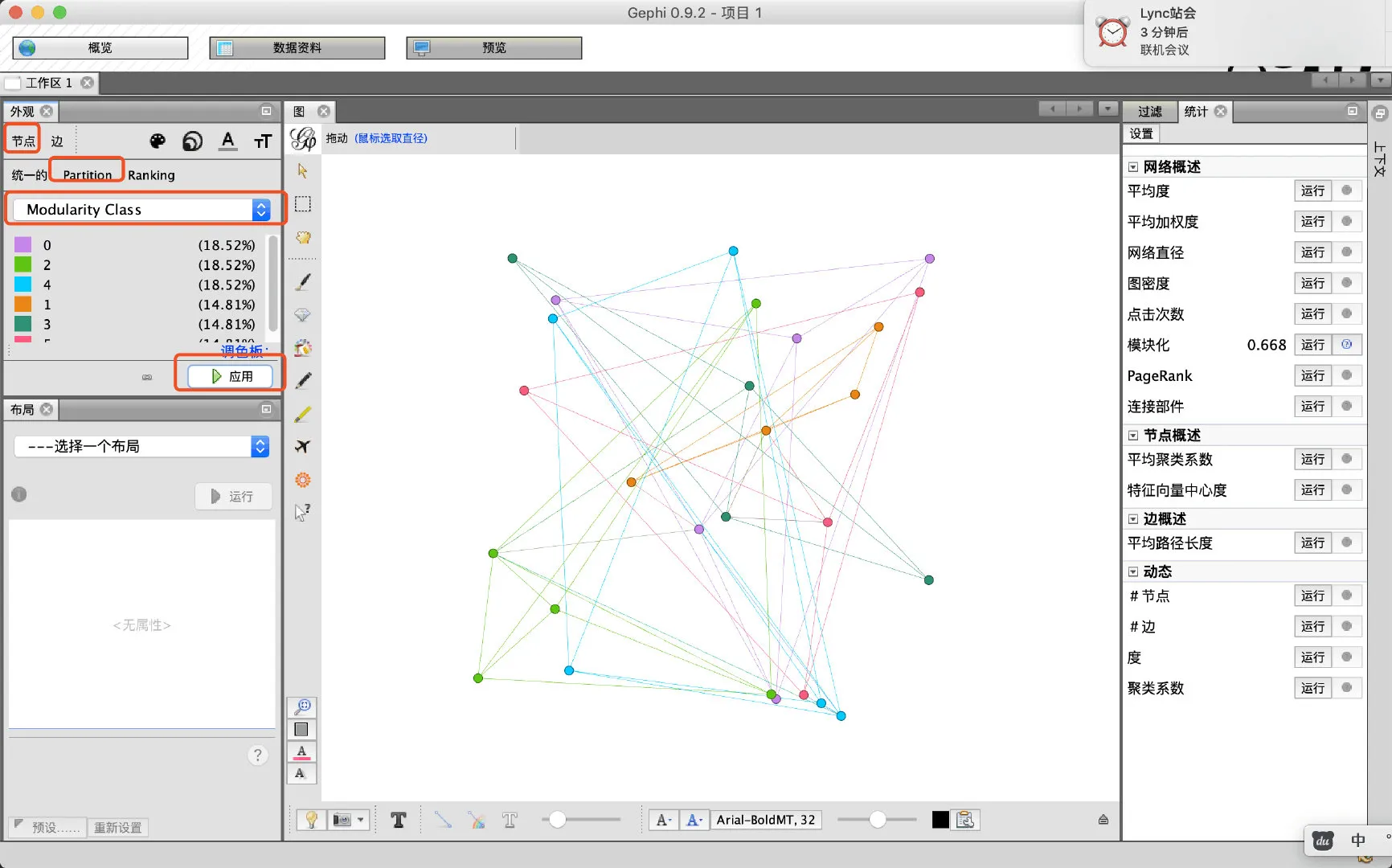
- 在图中展示结果,给节点上色
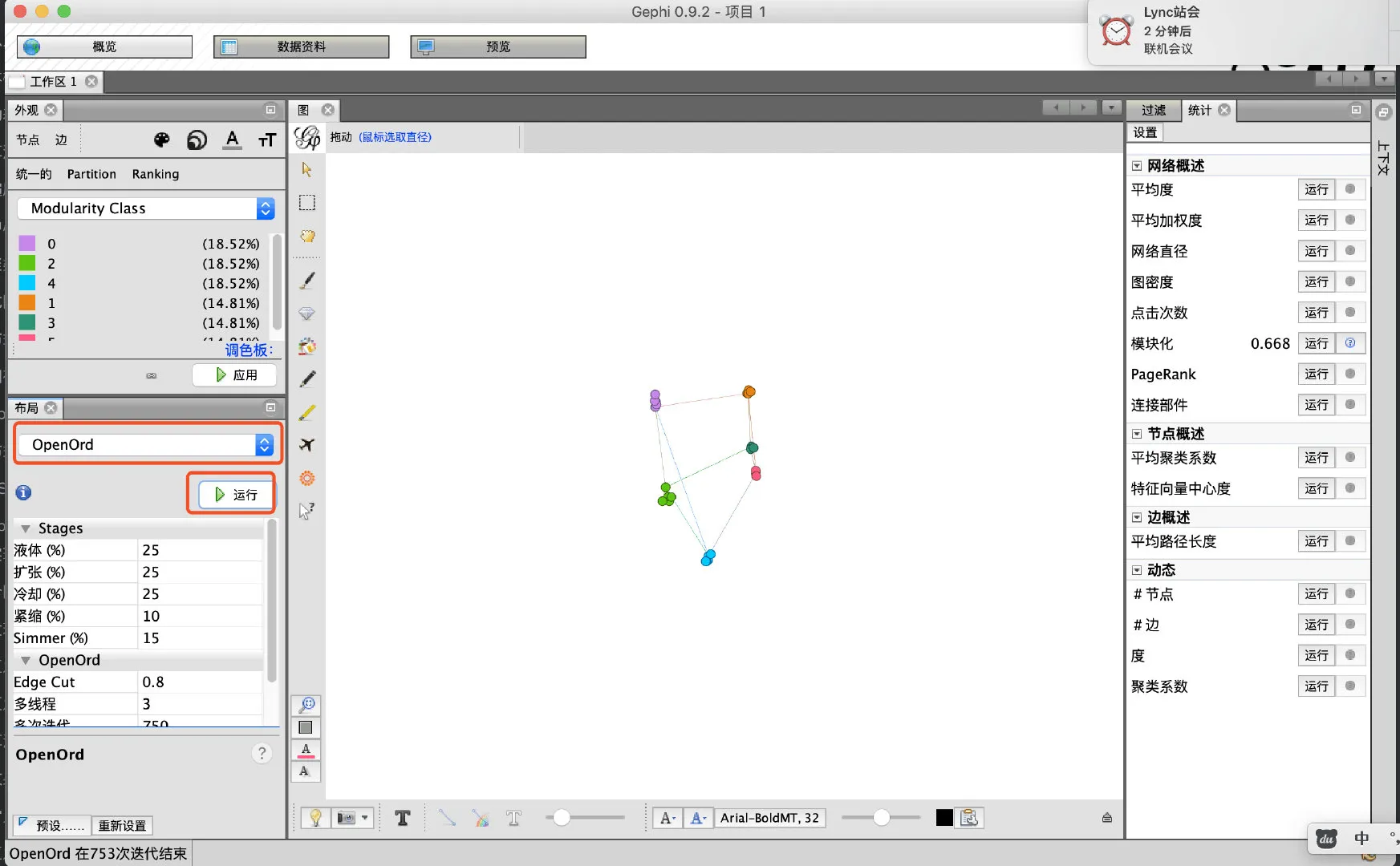
- 挑选一直算法尝试调整图的布局分布
总结
参考文档: